题目内容
2.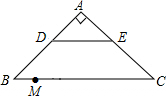 如图,在等腰直角三角形ABC中,AB=AC,斜边BC=20,点D,E分别是AB,AC的中点,M是BC上一点,BM=3,点N是线段MC上的一个动点,DN与ME相交于点O,若△OMN是直角三角形,则MN的长是2或$\frac{49}{12}$.
如图,在等腰直角三角形ABC中,AB=AC,斜边BC=20,点D,E分别是AB,AC的中点,M是BC上一点,BM=3,点N是线段MC上的一个动点,DN与ME相交于点O,若△OMN是直角三角形,则MN的长是2或$\frac{49}{12}$.
分析 如图作DN1⊥BC于N1交EM于O1,作EH⊥BC于H.则四边形DEHN1是矩形.求出MN1即可;作DN2⊥EM交EM于O2,交BC于N2,此时△MN2O2是直角三角形,求出MN2即可;
解答 解:如图作DN1⊥BC于N1交EM于O1,作EH⊥BC于H.则四边形DEHN1是矩形.
∵BC=20,AD=DB,AE=EC,
∴DE=$\frac{1}{2}$BC=10,易知EH=CH=BN1=DN1=5,
∵BM=3,
∴MN1=BN1-BM=5-3=2,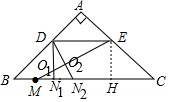
∴当MN1=2时,△MN1O1是直角三角形.
作DN2⊥EM交EM于O2,交BC于N2,此时△MN2O2是直角三角形,
∵△DN1N2∽△MHE,
∴$\frac{D{N}_{1}}{MH}$=$\frac{{N}_{1}{N}_{2}}{EH}$,
∴N1N2=$\frac{25}{12}$,
∴MN2=2+$\frac{25}{12}$=$\frac{49}{12}$.
∴当MN=2或$\frac{49}{12}$时,△MNO是直角三角形.
故答案为2或$\frac{49}{12}$.
点评 本题考查的是三角形中位线定理、等腰直角三角形的性质、矩形的判定和性质,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,正确寻找相似三角形解决问题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
17.李老师新买了一辆小轿车,为了掌握车的耗油情况,在连续两次加油时做了如下工作:
(1)把油箱加满油;
(2)记录了两次加油时的累积里程(注:“累积里程”指汽车从出厂开始累积行驶的路程).以下是李老师连续两次加油时的记录:
则在这段时间内,该车每100千米平均耗油量为( )
(1)把油箱加满油;
(2)记录了两次加油时的累积里程(注:“累积里程”指汽车从出厂开始累积行驶的路程).以下是李老师连续两次加油时的记录:
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
| 2017年3月18日 | 15 | 1200 |
| 2017年3月28日 | 30 | 1500 |
| A. | 15升 | B. | 10升 | C. | 7.5升 | D. | 5升 |
14.若a=$\frac{1}{2}$,b=-2,则代数式4a2+b2的值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
12.小红和小丽以大树为起点,小红向东走10米记作+10米,小丽向西走8米记作-8米,小红和小丽相距( )米.
| A. | 8米 | B. | 10米 | C. | 18米 | D. | 无法确定 |
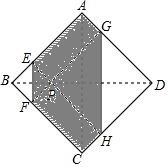 如图,正方形纸片ABCD的边长为2,翻折∠B、∠D.使两个直角的顶点重合于直线BD上一点P.EF与GH为折痕.若BP=$\frac{1}{4}$AC,则图中阴影部分的六边形AEFCHG的面积为$\frac{11}{4}$.
如图,正方形纸片ABCD的边长为2,翻折∠B、∠D.使两个直角的顶点重合于直线BD上一点P.EF与GH为折痕.若BP=$\frac{1}{4}$AC,则图中阴影部分的六边形AEFCHG的面积为$\frac{11}{4}$. 图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是4平方厘米.
图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是4平方厘米.