题目内容
如图，直线CD⊥AB，垂足为O，射线OE在∠AOD内部，∠COE：∠BOE=5：7，求∠AOE：∠DOE．考点：垂线
专题：
分析：根据已知条件可以设∠COE=5x，∠BOE=7x，利用周角的定义易求x的值．则根据图中角与角间的和差关系分别求得∠AOE、∠DOE的值，然后求其比值即可．
解答：解：设∠COE=5x，∠BOE=7x，则5x+7x+∠BOC=360°
∵CD⊥AB，
∴∠BOC=∠AOC=∠BOD=90°
∴12x+90°=360°，则x=22.5°
∴∠AOE=∠COE-∠AOC=5x-90°=22.5°，∠DOE=∠BOE-∠BOD=7x-90°=67.5°
∴∠AOE：∠DOE=1：3
∵CD⊥AB，
∴∠BOC=∠AOC=∠BOD=90°
∴12x+90°=360°，则x=22.5°
∴∠AOE=∠COE-∠AOC=5x-90°=22.5°，∠DOE=∠BOE-∠BOD=7x-90°=67.5°
∴∠AOE：∠DOE=1：3
点评：本题考查了垂线．要注意领会由垂直得直角这一要点．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
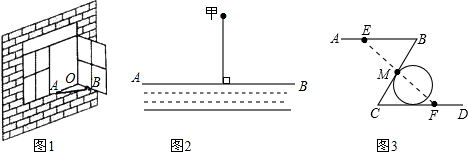
如图，AB∥CD．如果∠A+∠AMN=180°，那么MN与CD平行吗？说说你的理由．