题目内容
11. 如图,水库大坝的横断面是梯形ABCD,其中AB∥CD,大坝长100米,坝高20米,坡角α=45°,汛期来临前对其进行了加固,改造后的背水面坡度为1:$\sqrt{3}$,坝顶面加宽1米.
如图,水库大坝的横断面是梯形ABCD,其中AB∥CD,大坝长100米,坝高20米,坡角α=45°,汛期来临前对其进行了加固,改造后的背水面坡度为1:$\sqrt{3}$,坝顶面加宽1米.(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?($\sqrt{3}$=1.732).
分析 (1)作DG⊥AB于G,EH⊥AB于H,根据等腰直角三角形的性质求出AG,根据坡度的概念求出FH,结合图形计算即可;
(2)利用梯形的面积公式计算即可.
解答 解:(1)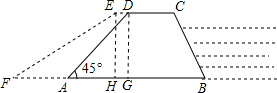 作DG⊥AB于G,EH⊥AB于H,
作DG⊥AB于G,EH⊥AB于H,
在Rt△ADG中,∠DAG=45°,DG=20,
∴AG=20,
∵背水面EF的坡度为1:$\sqrt{3}$,EH=20,
∴FH=20$\sqrt{3}$,
∴AF=FH+HG-AG=20$\sqrt{3}$+1-20=20$\sqrt{3}$-19≈15.64,
则加固后坝底增加的宽度AF的长约为15.64米;
(2)$\frac{1}{2}$(1+15.64)×20×100=16640,
答:完成这项工程需要土石16640立方米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度是坡面的铅直高度h和水平宽度l的比、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
20. 如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD( )
如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD( )
 如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD( )
如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠D=∠DCE | D. | ∠D+∠ACD=180° |
 图中每个小正方形的边长都是1,已知A点可用(3,2)表示
图中每个小正方形的边长都是1,已知A点可用(3,2)表示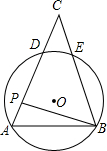 如图,⊙O经过△ABC的两个顶点A,B,与边AC,BC分别交于点D,E,点P从点A出发,沿A→D→E→C的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图大致是( )
如图,⊙O经过△ABC的两个顶点A,B,与边AC,BC分别交于点D,E,点P从点A出发,沿A→D→E→C的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图大致是( )