题目内容
9. 如图,AO⊥BO,CO⊥DO,∠AOD=4∠BOC,求∠BOC的度数.
如图,AO⊥BO,CO⊥DO,∠AOD=4∠BOC,求∠BOC的度数.
分析 根据垂直的性质,可得∠AOB和∠COD的度数,根据∠AOD=4∠BOC,可得答案.
解答 解:∵AO⊥BO,CO⊥DO,
∴∠AOB=∠COD=90°,
∵∠AOD=4∠BOC,
∴4∠BOC=90°+90°+∠BOC,
解得:∠BOC=60°.
点评 本题考查了垂线,利用了垂线的定义,角的和差计算是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
14.下列事件中,属于必然事件的是( )
| A. | 二次函数的图象是抛物线 | |
| B. | 任意一个一元二次方程都有实数根 | |
| C. | 三角形的外心在三角形的外部 | |
| D. | 投掷一枚均匀的硬币100次,正面朝上的次数为50次 |
18.已知点A(-1,y1)、B(0.5,y2)在反比例函数$y=\frac{5}{x}$图象上,则有( )
| A. | y1<0<y2 | B. | y2<0<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
19.已知∠A是锐角,且sinA=$\frac{3}{5}$,则tanA的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
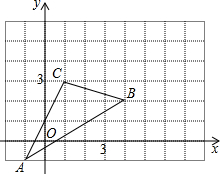 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,