题目内容
1.已知扇形的弧长为2πcm,圆心角为120°,则扇形的面积为3πcm2.分析 首先运用弧长公式求出扇形的半径,运用扇形的面积公式直接计算,即可解决问题.
解答 解:设该扇形的弧长为λ,半径为μ,圆心角为α°,
则$\frac{απμ}{180}=2π$,而α=120,
解得:μ=3,
∴该扇形的面积=$\frac{120π•{3}^{2}}{360}$=3π(cm2),
故答案为3π.
点评 该题主要考查了扇形的面积公式、弧长公式等知识点及其应用问题;应牢固掌握扇形的面积公式、弧长公式,这是灵活运用、解题的基础和关键.

练习册系列答案
相关题目
11.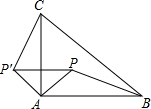 如图,△ABC中,∠BAC=90°,AC=AB,P是△ABC內一点,PA=1,连PB,把△ABP绕点A逆时针旋转90°后,点P的对应点为P′,则点P与点P′之间的距离为( )
如图,△ABC中,∠BAC=90°,AC=AB,P是△ABC內一点,PA=1,连PB,把△ABP绕点A逆时针旋转90°后,点P的对应点为P′,则点P与点P′之间的距离为( )
 如图,△ABC中,∠BAC=90°,AC=AB,P是△ABC內一点,PA=1,连PB,把△ABP绕点A逆时针旋转90°后,点P的对应点为P′,则点P与点P′之间的距离为( )
如图,△ABC中,∠BAC=90°,AC=AB,P是△ABC內一点,PA=1,连PB,把△ABP绕点A逆时针旋转90°后,点P的对应点为P′,则点P与点P′之间的距离为( )| A. | A$\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
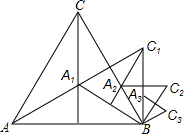 如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.
如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.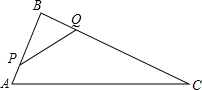 如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?
如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似? 如图,AO⊥BO,CO⊥DO,∠AOD=4∠BOC,求∠BOC的度数.
如图,AO⊥BO,CO⊥DO,∠AOD=4∠BOC,求∠BOC的度数. 如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=35°,则∠AOC=55°.
如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=35°,则∠AOC=55°. 如图所示,在△ABC中,∠A=90°,BD平分∠ABC,AD=2cm,AB+BC=8,S△ABC=8cm2.
如图所示,在△ABC中,∠A=90°,BD平分∠ABC,AD=2cm,AB+BC=8,S△ABC=8cm2.