题目内容
17．直线l1与l2相交于点O，对于平面内任意一点M，若点M到直线l1的距离为1，且到直线l2的距离为2，则符合条件的点M的个数是4．分析 由于到直线l1的距离是1的点在与直线l1平行且与l1的距离是1的两条平行线a1、a2上，到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线b1、b2上，它们有4个交点，即为所求．
解答 解：如图：
∵到直线l1的距离是1的点在与直线l1平行且与l1的距离是1的两条平行线a1、a2上，
到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线b1、b2上，
∴符合条件的点是M1、M2、M3、M4，一共4个．
故答案为：4．
点评 本题考查了点到直线的距离，两平行线之间的距离的定义，掌握到一条直线的距离等于定长k的点在与已知直线相距k的两条平行线上是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
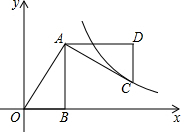如图，平面直角坐标中，OB在x轴上，∠ABO=90°，点A的坐标为（2，4），将△AOB绕点A逆时针旋转90°，点O的对应点C恰好落在双曲线y=$\frac{k}{x}$（x＞0）上，则k的值为（ ）
已知直线y=$-\frac{3}{4}x+3$与直线y=$kx-\frac{16}{3}$交于x轴上的同一个点A，直线y=$-\frac{3}{4}x+3$与y轴交于点B，直线y=$kx-\frac{16}{3}$与y轴的交点为C．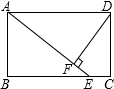
如图，矩形ABCD中，E为BC上一点，DF⊥AE于点F，求证：△ABE∽△DFA．
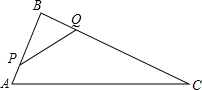如图，在△ABC中，AB=8cm，BC=16cm，点P从点A开始沿AB向点B以2m/s的速度运动，点Q从点B开始沿BC边向点C以4cm/s的速度运动，如果P、Q分别从A、B同时出发，4秒后停止运动．则在开始运动后第几秒，△BPQ与△BAC相似？
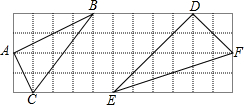如图所示，方格纸中每个小正方形的边长为1，△ABC和△DEF的顶点都在方格纸的格点上，判断△ABC和△DEF是否相似，并说明理由．
如图，AO⊥BO，CO⊥DO，∠AOD=4∠BOC，求∠BOC的度数．