题目内容
14.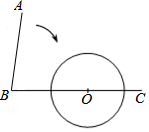 如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,$\frac{1}{2}$OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转( )
如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,$\frac{1}{2}$OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转( )| A. | 40°或80° | B. | 50°或110° | C. | 50°或100° | D. | 60°或120° |
分析 设旋转后与⊙O相切于点D,连接OD,则可求得∠DBO=30°,再利用角的和差可求得∠ABD的度数.
解答  解:
解:
如图,设旋转后与⊙O相切于点D,连接OD,
∵OD=$\frac{1}{2}$OB,
∴∠OBD=30°,
∴当点D在射线BC上方是时,∠ABD=∠ABC-∠OBD=80°-30°=50°,
当点D在射线BC下方时,∠ABD=∠ABC+∠OBD=80°+30°=110°,
故选B.
点评 本题主要考查切线的性质和旋转的性质,利用过切点的半径与切线垂直求得∠OBD的度数是解题的关键,注意分类讨论.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
2.甲班、乙班两班为举办“浓情‘苹’安夜”联欢活动,分别选派班委成员到集市上购买苹果,苹果的价格如下:
(1)甲班分两次共购买苹果70kg(第二次多于第一次),共付出255元;乙班一次购买苹果70kg.
①乙班买苹果付了210元;
②乙班比甲班少付了45元;
③甲班第一次、第二次分别购买苹果多少千克?请写出计算过程.
(2)若甲班分两次购买苹果70kg(第二次多于第一次),并且第一次购买不少于10kg,如何购买最省钱?最省的钱是多少?请直接写出最省钱的购买方案.
| 购买苹果数 | 不超过30kg | 30kg以上 且不超过50kg | 50kg以上 |
| 每千克价格 | 4元 | 3.5元 | 3元 |
①乙班买苹果付了210元;
②乙班比甲班少付了45元;
③甲班第一次、第二次分别购买苹果多少千克?请写出计算过程.
(2)若甲班分两次购买苹果70kg(第二次多于第一次),并且第一次购买不少于10kg,如何购买最省钱?最省的钱是多少?请直接写出最省钱的购买方案.
3.一元二次方程x2-2x=0的根是( )
| A. | x1=0,x2=2 | B. | x1=1,x2=2 | C. | x1=1,x2=-2 | D. | x1=0,x2=-2 |
4.已知⊙O的半径R=$\sqrt{3}$cm,点O到直线l的距离为d,如果直线l与⊙O有公共点,那么( )
| A. | d≤$\sqrt{3}$cm | B. | d$<\sqrt{3}$cm | C. | d$≥\sqrt{3}$cm | D. | d$>\sqrt{3}$cm |
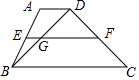 如图,梯形ABCD中,AD∥BC,对角线BD与中位线EF交于点G,若AD=2,EF=5,那么FG=4.
如图,梯形ABCD中,AD∥BC,对角线BD与中位线EF交于点G,若AD=2,EF=5,那么FG=4.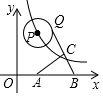 如图,动点P在函数y=$\frac{16}{x}$(x>0)的图象上移动,⊙P半径为2,A(3,0),B(6,0),点Q是⊙P上的动点,点C是QB的中点,则AC的最小值是2$\sqrt{2}$-1.
如图,动点P在函数y=$\frac{16}{x}$(x>0)的图象上移动,⊙P半径为2,A(3,0),B(6,0),点Q是⊙P上的动点,点C是QB的中点,则AC的最小值是2$\sqrt{2}$-1.
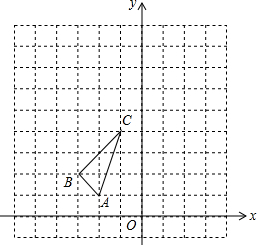 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1)、B(-3,2)、C(-1,4).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1)、B(-3,2)、C(-1,4).