题目内容
5.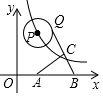 如图,动点P在函数y=$\frac{16}{x}$(x>0)的图象上移动,⊙P半径为2,A(3,0),B(6,0),点Q是⊙P上的动点,点C是QB的中点,则AC的最小值是2$\sqrt{2}$-1.
如图,动点P在函数y=$\frac{16}{x}$(x>0)的图象上移动,⊙P半径为2,A(3,0),B(6,0),点Q是⊙P上的动点,点C是QB的中点,则AC的最小值是2$\sqrt{2}$-1.
分析 取点P(4,4),连接OP交⊙P于点Q′,连接BQ′,取BQ′的中点C′,连接AC′.因为OA=AB、CB=CQ,所以AC=$\frac{1}{2}$OQ,所以当OP最小时,OQ、AC最小,Q运动到Q′时,OQ最小,由此即可解决问题.
解答 解:取点P(4,4),连接OP交⊙P于点Q′,连接BQ′,取BQ′的中点C′,连接AC′,此时AC′最小.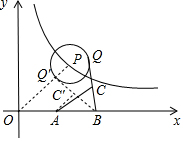
设点P的坐标为(x,$\frac{16}{x}$),则OP=$\sqrt{{x}^{2}+(\frac{16}{x})^{2}}$≥$\sqrt{2x•\frac{16}{x}}$=4$\sqrt{2}$,当x=$\frac{16}{x}$=4时,取等号.
∵A(3,0),B(6,0),点C是QB的中点,
∴OA=AB,CB=CQ,
∴AC=$\frac{1}{2}$OQ.
当Q运动到Q′时,OQ最小,
此时AC的最小值AC′=$\frac{1}{2}$OQ′=$\frac{1}{2}$(OP-PQ′)=2$\sqrt{2}$-1.
故答案为:2$\sqrt{2}$-1.
点评 本题考查了反比例函数图象上点的坐标特征、两点间的距离公式、完全平方公式、三角形中位线定理、最小值问题等知识,解题的关键是根据完全平方公式找出OP最小时点P的坐标并确定当AC最小时点Q的位置.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.有一块长为m,宽为n的长方形铝片,四角各截去一个相同的边长为x的小正方形,折起来做成一个没有盖的盒子,则此盒子的体积可表示为( )
| A. | x(m-x)(n-x) | B. | x2(m-x)(n-x) | C. | $\frac{1}{3}$x(m-2n)(n-2x) | D. | x(m-2x)(n-2x) |
20.下列图形,对称轴最多的是( )
| A. | 正方形 | B. | 等边三角形 | C. | 角 | D. | 线段 |
14.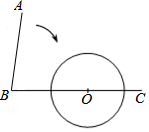 如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,$\frac{1}{2}$OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转( )
如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,$\frac{1}{2}$OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转( )
 如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,$\frac{1}{2}$OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转( )
如图,∠ABC=80°,O为射线BC上一点,以点O为圆心,$\frac{1}{2}$OB长为半径作⊙O,要使射线BA与⊙O相切,应将射线绕点B按顺时针方向旋转( )| A. | 40°或80° | B. | 50°或110° | C. | 50°或100° | D. | 60°或120° |
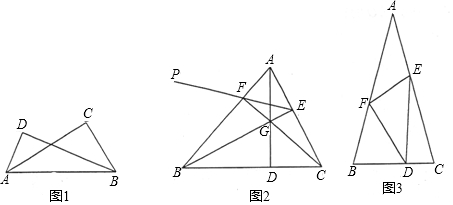
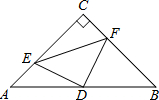 如图,在△ABC中,∠C=90°,AC=BC=5,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF,在此运动变化的过程中,△CEF周长的最小值是5+$\frac{5\sqrt{2}}{2}$.
如图,在△ABC中,∠C=90°,AC=BC=5,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF,在此运动变化的过程中,△CEF周长的最小值是5+$\frac{5\sqrt{2}}{2}$.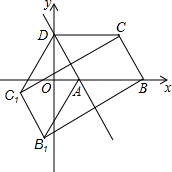 如图,已知?ABCD的三个顶点A(n,0),B(m,0),D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D.
如图,已知?ABCD的三个顶点A(n,0),B(m,0),D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D.