题目内容
2. 如图,已知菱形ABCD对角线交于点O,AE⊥CD于E,AE=OD,则∠CAE=30°.
如图,已知菱形ABCD对角线交于点O,AE⊥CD于E,AE=OD,则∠CAE=30°.
分析 由四边形ABCD为菱形,得到对角线互相垂直,进而得到一对直角相等,再由对顶角相等,得到三角形AFO与三角形DFE相似,利用相似三角形对应角相等得到一对角相等,利用ASA得到三角形AEC与三角形DOC全等,利用全等三角形对应边相等得到AC=CD,进而确定出三角形ACD为等边三角形,利用等边三角形的性质及三线合一性质即可求出所求角的度数.
解答  解:∵菱形ABCD,
解:∵菱形ABCD,
∴AC⊥BD,AD=DC,
∵AE⊥CD,
∴∠AEC=∠DOC=90°,
∵∠AOD=∠AED=90°,∠AFO=∠DFE,
∴△AFO∽△DFE,
∴∠CAE=∠CDO,
在△AEC和△DOC中,
$\left\{\begin{array}{l}{∠CAE=∠CDO}\\{AE=OD}\\{∠AEC=∠DOC}\end{array}\right.$,
∴△AEC≌△DOC(ASA),
∴AC=CD,
∴AC=CD=AD,即△ACD为等边三角形,
∵AE⊥CD,
∴AE为∠CAD的平分线,
则∠CAE=30°.
故答案为:30°.
点评 此题考查了菱形的性质,全等三角形的判定与性质,以及等边三角形的判定与性质,熟练掌握菱形的性质是解本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
11.下列是一元一次方程的是( )
| A. | y=2x+1 | B. | 3a+3 | C. | 2x-3x=6 | D. | 2x=2x+1 |
 如图所示,木工师傅用角尺画出工件边缘的两条垂线,这两条垂线平行吗?为什么?
如图所示,木工师傅用角尺画出工件边缘的两条垂线,这两条垂线平行吗?为什么?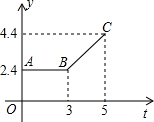 如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.