题目内容
20.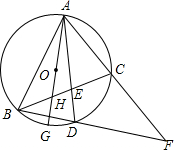 如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,连结CD,延长AC,BD,相交于点F.现给出下列结论:
如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,连结CD,延长AC,BD,相交于点F.现给出下列结论:①若AD=5,BD=2,则DE=$\frac{2}{5}$;
②∠ACB=∠DCF;
③△FDA∽△FCB;
④若直径AG⊥BD交BD于点H,AC=FC=4,DF=3,则cosF=$\frac{41}{48}$;
则正确的结论是( )
| A. | ①③ | B. | ②③④ | C. | ③④ | D. | ①②④ |
分析 ①只需证明△BDE∽△ADB,运用对应线段成比例求解即可;
②连接CD,假设∠ACB=∠DCF,推出与题意不符即可判断;
③由公共角和同弧所对的圆周角相等即可判断;
④先证明△FCD∽△FBA,求出BD的长度,根据垂径定理求出DH,结合三角函数即可求解.
解答 解:①如图1,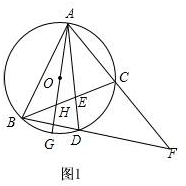
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠CAD=∠CBD,
∴∠BAD=∠CBD,
∵∠BDE=∠BDE,
∴△BDE∽△ADB,
∴$\frac{BD}{AD}=\frac{DE}{BD}$,
由AD=5,BD=2,可求DE=$\frac{4}{5}$,
①不正确;
②如图2,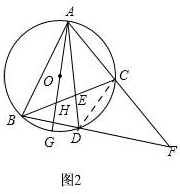
连接CD,
∠FCD+∠ACD=180°,∠ACD+∠ABD=180°,
∴∠FCD=∠ABD,
若∠ACB=∠DCF,因为∠ACB=∠ADB,
则有:∠ABD=∠ADB,与已知不符,
故②不正确;
③如图3,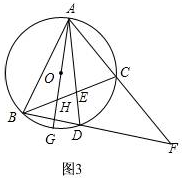
∵∠F=∠F,∠FAD=∠FBC,
∴△FDA∽△FCB;
故③正确;
④如图4,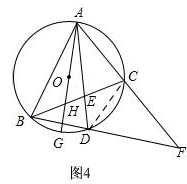
连接CD,由②知:∠FCD=∠ABD,
又∵∠F=∠F,
∴△FCD∽△FBA,
∴$\frac{FC}{FB}=\frac{FD}{FA}$,
由AC=FC=4,DF=3,可求:AF=8,FB=$\frac{32}{3}$,
∴BD=BF-DF=$\frac{23}{3}$,
∵直径AG⊥BD,
∴DH=$\frac{23}{6}$,
∴FH=$\frac{41}{6}$,
∴cosF=$\frac{FH}{AF}$=$\frac{41}{48}$,
故④正确;
故选:C.
点评 此题主要考查圆的综合问题,熟悉圆的相关性质,会证明三角形相似并解决相关问题,能灵活运用垂径定理和三角函数是解题的关键.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
11.下列是一元一次方程的是( )
| A. | y=2x+1 | B. | 3a+3 | C. | 2x-3x=6 | D. | 2x=2x+1 |
15.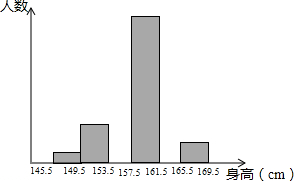 为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
(1)中m和n表示的数分别是多少?
(2)将如表中的数据画成频数分布直方图.
(3)如果全校有2500名女生,则身高在161.5cm以上的约有多少人?
 为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)(1)中m和n表示的数分别是多少?
(2)将如表中的数据画成频数分布直方图.
(3)如果全校有2500名女生,则身高在161.5cm以上的约有多少人?
| 组别 | 人数 | 百分比 |
| 145.5~149.5 | 1 | 2% |
| 149.5~153.5 | 4 | 8% |
| 153.5~157.5 | m | 40% |
| 157.5~161.5 | 15 | 30% |
| 161.5~165.5 | 8 | n |
| 165.5~169.5 | 2 | 4% |
| 合计 | 50 | 100% |
 如图,已知∠A=∠1,∠C=∠D.试说明FD∥BC.
如图,已知∠A=∠1,∠C=∠D.试说明FD∥BC.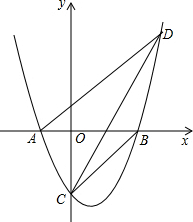 已知抛物线y=ax2+bx+c与x轴相交于点A(-1,0)和点B(4,0),与y轴相交于点C(0,-4)
已知抛物线y=ax2+bx+c与x轴相交于点A(-1,0)和点B(4,0),与y轴相交于点C(0,-4)