题目内容
20．
如图，在△ABC中，AB=6，AC=10，点D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长为（ ）| A． | 16 | B． | 12 | C． | 10 | D． | 8 |
分析 根据线段中点的概念求出AD、AF，根据三角形中位线定理求出DE、EF，计算即可．
解答 解：∵点D，E，F分别是AB，BC，AC的中点，
∴AD=$\frac{1}{2}$AB=3，AF=$\frac{1}{2}$AC=5，DE=$\frac{1}{2}$AC=5，EF=$\frac{1}{2}$AB=3，
∴四边形ADEF的周长=AD+DE+EF+FA=3+5+5+3=16，
故选：A．
点评 本题考查的是三角形中位线定理的应用，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
练习册系列答案
相关题目
8．当a为任意实数时，下列各式总有意义的是（ ）
| A． | $\sqrt{{a}^{2}}$ | B． | $\sqrt{a}$ | C． | $\sqrt{\frac{1}{{a}^{2}}}$ | D． | $\sqrt{-a}$ |
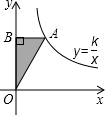如图，点A是反比例函数y=$\frac{k}{x}$（x≠0）的图象上一点，AB⊥y轴于B，若△ABO的面积为4，则k的值为8．
在平面直角坐标xOy中，直线y=kx-3（k≠0）与直线y=mx（m≠0）的一个交点为A（1，-2），与x轴交于点B．
如图有一张最长边长为8，最小边长为4的直角三角形纸片，沿图中所示的中位线剪开后，将两部分拼成一个四边形，所得四边形的周长是8+4$\sqrt{3}$或16．