题目内容
15.已知|2x-1|+(y+3)2=0,且2x+my=4,则m=-1.分析 利用非负数的性质求出x与y的值,代入已知等式即可求出m的值.
解答 解:∵|2x-1|+(y+3)2=0,
∴2x-1=0且y+3=0,即x=$\frac{1}{2}$,y=-3,
代入2x+my=4得:2×$\frac{1}{2}$-3m=4,
解得:m=-1.
故答案为:-1.
点评 此题考查了二元一次方程的解,以及非负数的性质,求出x与y的值是解本题的关键.

练习册系列答案
相关题目
5.若$\sqrt{x+y-1}$+(y+2)2=0,则x-y的值为( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
20. 如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
 如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )| A. | 16 | B. | 12 | C. | 10 | D. | 8 |
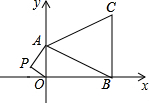 如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.
如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.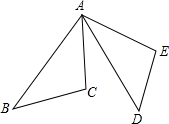 如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗?
如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗?