题目内容
12. 在平面直角坐标xOy中,直线y=kx-3(k≠0)与直线y=mx(m≠0)的一个交点为A(1,-2),与x轴交于点B.
在平面直角坐标xOy中,直线y=kx-3(k≠0)与直线y=mx(m≠0)的一个交点为A(1,-2),与x轴交于点B.(1)求m的值和点B的坐标;
(2)不解不等式,直接写kx-3<mx的解集.
分析 (1)把A(1,-2)分别代入直线y=kx-3与直线y=mx,得出m与k的值,进而求出B的坐标;
(2)在同一坐标系中画出两函数的图象,观察直线y=x-3落在直线y=-2x下方的部分对应的x的取值范围即为所求.
解答  解:(1)∵直线y=kx-3(k≠0)与直线y=mx(m≠0)的一个交点为A(1,-2),
解:(1)∵直线y=kx-3(k≠0)与直线y=mx(m≠0)的一个交点为A(1,-2),
∴k-3=-2,m=-2,
∴k=1,
∴y=x-3,
当y=0时,x-3=0,解得x=3,
∴B(3,0);
(2)如图,当x<1时,直线y=x-3 的图象落在直线y=-2x的下方,即x-3<-2x,
所以x-3<-2x的解集是x<1.
点评 此题考查了一次函数与一元一次不等式以及待定系数法求函数的解析式.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
2.某超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表统计了近两周的销售情况:
(1)求A、B两种型号的电风扇每台的销售价分别是多少元?
(2)若超市准备用不超过5250元的金额再采购这两种型号的电风扇共30台,
①求A种型号的电风扇最多能采购多少台?
②超市销售完这30台电风扇是否能实现利润不低于1240元的目标?若能实现,请写出相应的采购方案,若不能实现,请说明理由.
(进价、售价均保持不变,利润=销售收入-进货成本)
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800 |
| 第二周 | 6台 | 8台 | 3180 |
(2)若超市准备用不超过5250元的金额再采购这两种型号的电风扇共30台,
①求A种型号的电风扇最多能采购多少台?
②超市销售完这30台电风扇是否能实现利润不低于1240元的目标?若能实现,请写出相应的采购方案,若不能实现,请说明理由.
(进价、售价均保持不变,利润=销售收入-进货成本)
20. 如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
 如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )| A. | 16 | B. | 12 | C. | 10 | D. | 8 |
17. 随地球自转,一天中太阳东升西落,太阳经过某地天空的最高点时为此地的“地方时间”12点,因此,不同经线上具有不同的“地方时间”.两个地区“地方时间”之间的差称为这两个地区的时差.
随地球自转,一天中太阳东升西落,太阳经过某地天空的最高点时为此地的“地方时间”12点,因此,不同经线上具有不同的“地方时间”.两个地区“地方时间”之间的差称为这两个地区的时差.
如图表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)下表是同一时刻的北京和首尔的时间,请填写完整.
(2)设北京时间为x(时),首尔时间为y(时),0≤x≤12时,求y关于x的函数表达式.
 随地球自转,一天中太阳东升西落,太阳经过某地天空的最高点时为此地的“地方时间”12点,因此,不同经线上具有不同的“地方时间”.两个地区“地方时间”之间的差称为这两个地区的时差.
随地球自转,一天中太阳东升西落,太阳经过某地天空的最高点时为此地的“地方时间”12点,因此,不同经线上具有不同的“地方时间”.两个地区“地方时间”之间的差称为这两个地区的时差.如图表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)下表是同一时刻的北京和首尔的时间,请填写完整.
| 北京时间 | 7:30 | 11:15 |
| 首尔时间 | 8:30 | 12:15 |
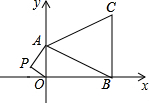 如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.
如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.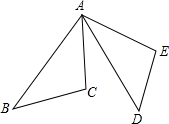 如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗?
如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗?
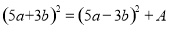 ,则A=( )
,则A=( )