题目内容
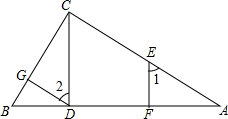 已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC
已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC证明:∵EF⊥AB CD⊥AB
∴∠EFA=∠CDA=90°(垂直定义)
∠1=∠
∴EF∥CD
∴∠1=∠2(已知)
∴∠2=∠ACD(等量代换)
∴DG∥AC
∴∠DGB=∠ACB
∵AC⊥BC(已知)
∴∠ACB=90°(垂直定义)
∴∠DGB=90°即DG⊥BC.
考点:平行线的判定与性质,垂线
专题:推理填空题
分析:根据垂直定义求出∠EFA=∠CDA=90°,求出∠1=∠ACD,推出EF∥CD,根据平行线的性质得出∠2=∠ACD,推出DG∥AC,根据平行线的性质推出∠ACB=∠DGB即可.
解答:证明:∵EF⊥AB,CD⊥AB(已知),
∴∠EFA=∠CDA=90°(垂直定义),
∴EF∥CD(同位角相等,两直线平行),
∴∠1=∠ACD(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠2=∠ACD(等量代换),
∴DG∥AC(内错角相等,两直线平行),
∴∠DGB=∠ACB(两直线平行,同位角相等),
∵AC⊥CB,
∴∠ACB=90°,
∴∠DGB=90°,
即DG⊥BC,
故答案为:已知,ACD,(两直线平行,同位角相等),(内错角相等,两直线平行),(两直线平行,同位角相等).
∴∠EFA=∠CDA=90°(垂直定义),
∴EF∥CD(同位角相等,两直线平行),
∴∠1=∠ACD(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠2=∠ACD(等量代换),
∴DG∥AC(内错角相等,两直线平行),
∴∠DGB=∠ACB(两直线平行,同位角相等),
∵AC⊥CB,
∴∠ACB=90°,
∴∠DGB=90°,
即DG⊥BC,
故答案为:已知,ACD,(两直线平行,同位角相等),(内错角相等,两直线平行),(两直线平行,同位角相等).
点评:本题考查了平行线的判定和性质,三角形内角和定理,垂直定义的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
 如图,直线y=kx+b与x轴相交于点(-4,0),则y<0时,x的取值范围是( )
如图,直线y=kx+b与x轴相交于点(-4,0),则y<0时,x的取值范围是( )| A、x<-4 | B、x>0 |
| C、x>-4 | D、x<0 |
若(x-3)0-2(3x-6)-2有意义,则x的取值范围是( )
| A、x>3 |
| B、x≠3且x≠2 |
| C、x≠3或x≠2 |
| D、x<2 |
若n≠0,a<b,则下列不等式中成立的是( )
| A、an<bn | ||||
| B、an2<bn2 | ||||
C、
| ||||
D、-
|
若函数y=(3-m)xm2-8是正比例函数,则m的值是( )
| A、-3 | B、3 | C、±3 | D、-1 |
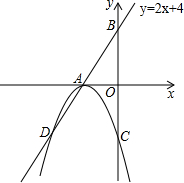 如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,-4).
如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,-4).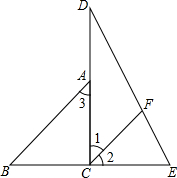 将一副三角板拼成如图的图形,其中CD⊥BE于点C,∠D=30°,∠B=45°,且过点C作CF平分∠DCE交DE于点F.
将一副三角板拼成如图的图形,其中CD⊥BE于点C,∠D=30°,∠B=45°,且过点C作CF平分∠DCE交DE于点F. 如图,已知正方形ABCD的边长是2,∠EAF=m°,将∠EAF绕点A顺时针旋转,它的两边分别交BC、CD于点E、F,G是CB延长线上一点,且始终保持BG=DF.
如图,已知正方形ABCD的边长是2,∠EAF=m°,将∠EAF绕点A顺时针旋转,它的两边分别交BC、CD于点E、F,G是CB延长线上一点,且始终保持BG=DF.