题目内容
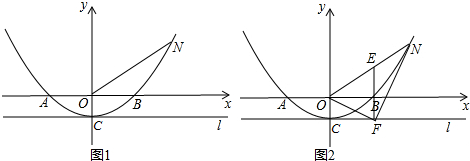
如图1,已知抛物线与坐标轴分别交于点A(-4,0)、B(4,0)、C(0,-2),过点C作平行于x轴的直线l.
(1)求抛物线的解析式;
(2)已知点N(8,6),直线l上是否存在点P,使得△OPN是以ON为直角边的直角三角形?若存在,求出所有满足条件的点P的坐标;若不存,请说明理由;
(3)如图2,设N(m,n)(m≠0)为抛物线上一动点,过ON的中点E作EF⊥l于点F,连接FO,FN.
①求证:∠OFN=90°;
②若△OFN是以ON为斜边的等腰直角三角形,请直接写出满足条件的点N的坐标(不必写出求解过程).
(1)求抛物线的解析式;
(2)已知点N(8,6),直线l上是否存在点P,使得△OPN是以ON为直角边的直角三角形?若存在,求出所有满足条件的点P的坐标;若不存,请说明理由;
(3)如图2,设N(m,n)(m≠0)为抛物线上一动点,过ON的中点E作EF⊥l于点F,连接FO,FN.
①求证:∠OFN=90°;
②若△OFN是以ON为斜边的等腰直角三角形,请直接写出满足条件的点N的坐标(不必写出求解过程).

考点:二次函数综合题
专题:
分析:(1)应用待定系数法即可求得.
(2)设出P点的坐标(m,-2),表示出OP2、ON2、PN2的值,分两种情况讨论,当∠PON=90°时,OP2+ON2=PN2,当∠PNO=90°时,PN2+ON2=OP2,即可求得.
(3)①先根据勾股定理求得OF2、NF2、NO2,然后根据勾股定理的逆定理即可判定;②根据OF2=NF2求出n的值即可求得m的值,从而求得N点的坐标.
(2)设出P点的坐标(m,-2),表示出OP2、ON2、PN2的值,分两种情况讨论,当∠PON=90°时,OP2+ON2=PN2,当∠PNO=90°时,PN2+ON2=OP2,即可求得.
(3)①先根据勾股定理求得OF2、NF2、NO2,然后根据勾股定理的逆定理即可判定;②根据OF2=NF2求出n的值即可求得m的值,从而求得N点的坐标.
解答:(1)解:设抛物线的解析式为y=ax2+bx+c,依题意得
解得
∴抛物线的解析式为y=
x2-2,
(2)存在;
设P点的坐标(m,-2),则OP2=22+m2=4+m2,ON2=62+82=100,PN2=(6+2)2+(8-m)2=m2-16m+128,
∵当∠PON=90°时,OP2+ON2=PN2,
∴4+m2+100=m2-16m+128,解得m=
,
∴P(
,-2),
∵当∠PNO=90°时,PN2+ON2=OP2,
∴m2-16m+128+100=4+m2,解得m=14,
∴P(14,-2)
(3)①证明;过N点作NG⊥X轴于G,
∵N(m,n),依题意得F(
,-2),
∴n=
m2-2,即m2=8n+16,
∴OF2=CF2+OC2=
+4=2n+8,
∴NF2=GF2=+NG2=
+(n+2)2=n2+6n+8,NO2=m2+n2=8n+16+n2,
∴OF2+NF2=ON2,
∴∠OFN=90°;
②N(-4,0)或N(4,0).
∵△OFN是以ON为斜边的等腰直角三角形,
∴OF=NF,
∵NF2=n2+6n+8,NO2=8n+16+n2,
∴OF2=2n+8,
∴n2+6n+8=2n+8,解得:n=0或n=-4(舍去),
∴0=
m2-2,解得:m=4,或m=-4,
∴N(-4,0)或N(4,0).
|
|
∴抛物线的解析式为y=
| 1 |
| 8 |
(2)存在;
设P点的坐标(m,-2),则OP2=22+m2=4+m2,ON2=62+82=100,PN2=(6+2)2+(8-m)2=m2-16m+128,
∵当∠PON=90°时,OP2+ON2=PN2,
∴4+m2+100=m2-16m+128,解得m=
| 3 |
| 2 |
∴P(
| 3 |
| 2 |
∵当∠PNO=90°时,PN2+ON2=OP2,
∴m2-16m+128+100=4+m2,解得m=14,
∴P(14,-2)
(3)①证明;过N点作NG⊥X轴于G,

∵N(m,n),依题意得F(
| m |
| 2 |
∴n=
| 1 |
| 8 |
∴OF2=CF2+OC2=
| m2 |
| 4 |
∴NF2=GF2=+NG2=
| m2 |
| 4 |
∴OF2+NF2=ON2,
∴∠OFN=90°;
②N(-4,0)或N(4,0).
∵△OFN是以ON为斜边的等腰直角三角形,
∴OF=NF,
∵NF2=n2+6n+8,NO2=8n+16+n2,
∴OF2=2n+8,
∴n2+6n+8=2n+8,解得:n=0或n=-4(舍去),
∴0=
| 1 |
| 8 |
∴N(-4,0)或N(4,0).
点评:本题考查了待定系数法求解析式,勾股定理以及勾股定理的逆定理,等腰直角三角形的性质等.

练习册系列答案
相关题目
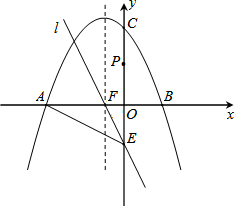 如图,抛物线C1:y=ax2+bx+4的图象与两坐标轴分别交于A、B、C三点,经过点E(0,-2)的直线l:y=kx-2(k≠0)与x轴、抛物线的对称轴x=-1交于点F.
如图,抛物线C1:y=ax2+bx+4的图象与两坐标轴分别交于A、B、C三点,经过点E(0,-2)的直线l:y=kx-2(k≠0)与x轴、抛物线的对称轴x=-1交于点F.
 如图所示的网络图中,每个小正方形的边长为1,△ABC的三个顶点都在格点上,把△ABC绕着A点逆时针旋转90°后得到△AB′C′.
如图所示的网络图中,每个小正方形的边长为1,△ABC的三个顶点都在格点上,把△ABC绕着A点逆时针旋转90°后得到△AB′C′.