题目内容
20.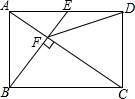 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 ①四边形ABCD是矩形,BE⊥AC,则∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB,故①正确;
②由AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,又AD∥BC,所以$\frac{AE}{BC}=\frac{AF}{FC}=\frac{1}{2}$,故②正确;
③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=$\frac{1}{2}$BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故③正确;
④根据三角函数的定义得到tan∠CAD=$\frac{\sqrt{2}}{2}$,故④错误;
⑤根据△AEF∽△CBF得到$\frac{EF}{BF}=\frac{AE}{BC}=\frac{1}{2}$,求出S△AEF=$\frac{1}{2}$S△ABF,S△ABF=$\frac{1}{6}$S矩形ABCDS四边形CDEF=S△ACD-S△AEF=$\frac{1}{2}$S矩形ABCD-$\frac{1}{12}$S矩形ABCD=$\frac{5}{12}$S矩形ABCD,即可得到S四边形CDEF=$\frac{5}{2}$S△ABF,故⑤正确.
解答 解:过D作DM∥BE交AC于N,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴$\frac{AE}{BC}=\frac{AF}{CF}$,
∵AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴$\frac{AF}{CF}$=$\frac{1}{2}$,
∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=$\frac{1}{2}$BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,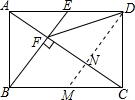
∴DF=DC,故③正确;
设AD=a,AB=b由△BAE∽△ADC,有$\frac{b}{a}=\frac{\frac{a}{2}}{b}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,
∴$\frac{b}{a}$=$\frac{\sqrt{2}}{2}$,
∵tan∠CAD=$\frac{CD}{AD}$=$\frac{b}{a}$,
∴tan∠CAD=$\frac{\sqrt{2}}{2}$,故④错误;
∵△AEF∽△CBF,
∴$\frac{EF}{BF}=\frac{AE}{BC}=\frac{1}{2}$,
∴S△AEF=$\frac{1}{2}$S△ABF,S△ABF=$\frac{1}{6}$S矩形ABCD
∴S△AEF=$\frac{1}{12}$S矩形ABCD,
又∵S四边形CDEF=S△ACD-S△AEF=$\frac{1}{2}$S矩形ABCD-$\frac{1}{12}$S矩形ABCD=$\frac{5}{12}$S矩形ABCD,
∴S四边形CDEF=$\frac{5}{2}$S△ABF,故⑤正确;
故选B.
点评 本题考查了相似三角形的判定和性质,矩形的性质,图形面积的计算,正确的作出辅助线是解题的关键.

| A. | 了解全校同学喜欢课程情况,对某班男生进行调查 | |
| B. | 了解某小区居民的防火意识,从每幢居民随机抽若干人进行调查 | |
| C. | 了解商场的平均日营业额,选在周末进行调查 | |
| D. | 了解杭州城区空气质量,在江干区设点调查 |
| A. | k>0,b>0 | B. | k>0,b≤0 | C. | k<0,b>0 | D. | k<0,b<0 |
| A. | 2 | B. | 5 | C. | 8 | D. | 10 |
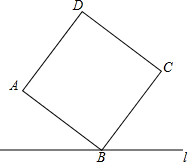 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的边长是$\sqrt{13}$.
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的边长是$\sqrt{13}$.