题目内容
2.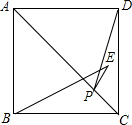 如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )
如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
分析 首先求得AB=1,从而可知BE=1,然后根据正方形的性质可知:PD=PB,从而可知:PD+PE=PB+PE,当E、P、B三点共线时,有最小值PD+PE=BE=1.
解答 解:连接PB.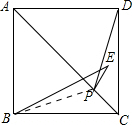
∵四边形ABCD为正方形,
∴AB=BC,∠B=90°.
∴AB=$\frac{\sqrt{2}}{2}AC$=$\frac{\sqrt{2}}{2}×\sqrt{2}$=1.
∵BE=AB,
∴BE=1.
∵四边形ABCD为正方形,
∴点B与点D关于AC对称.
∴PB=PD.
由点之间线段最短可知:当点E、P、B共线时,
PE+PD有最小值,PE+PD=PB+PE=BE=1.
故选:B.
点评 本题主要考查的是路径最短问题,利用正方形的对称性,得出PE+PD=PB+PE=BE是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
13.下列计算正确的是( )
| A. | x7+x2=x9 | B. | x12÷x6=x2 | C. | x2×x3=x6 | D. | (-x3)2=x6 |
10.一个平行四边形的两条对角线的长分别为8和10,则这个平行四边形边长不可能是( )
| A. | 2 | B. | 5 | C. | 8 | D. | 10 |
17.下列说法中,正确的是( )
| A. | 2是-4的算术平方根 | B. | -5是(-5)2的算术平方根 | ||
| C. | 16的平方根是±4 | D. | 27的立方根是±3 |
11.下列各式是最简二次根式的是( )
| A. | $\sqrt{5{x}^{2}}$ | B. | $\sqrt{0.9}$ | C. | $\sqrt{\frac{3}{7}}$ | D. | $\sqrt{{a}^{2}-3}$ |
 如图,DE∥AC,且∠1=∠2,试判断∠ADC与∠FGC有怎样的大小关系?并说明理由.
如图,DE∥AC,且∠1=∠2,试判断∠ADC与∠FGC有怎样的大小关系?并说明理由.


