题目内容
12．已知直线y=kx+b，若k+b=3，kb=-2，那该直线不经过的象限是第一象限．分析 首先根据k+b=-3、kb=2得到k、b的符号，再根据图象与系数的关系确定直线经过的象限，进而求解即可．
解答 解：∵k+b=-3，kb=2，
∴k＜0，b＜0，
∴直线y=kx+b经过二、三、四象限，即不经过第一象限．
故答案为第一象限．
点评 本题考查了一次函数图象与系数的关系，解题的关键是根据k、b之间的关系确定其符号．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
2．
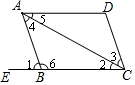如图，四边形ABCD，E是CB延长线上一点，下列推理正确的是（ ）
如图，四边形ABCD，E是CB延长线上一点，下列推理正确的是（ ）| A． | 如果∠1=∠2，那么AB∥CD | B． | 如果∠3=∠4，那么AD∥BC | ||
| C． | 如果AD∥BC，那么∠6+∠BAD=180° | D． | 如果∠6+∠BCD=180°，那么AD∥BC |
1．
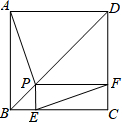如图，P为边长为2的正方形ABCD的对角线BD上任一点，过点P作PE⊥BC于点E，PF⊥CD于点F，连接EF．给出以下4个结论：①AP=EF；②AP⊥EF；③EF最短长度为$\sqrt{2}$；④若∠BAP=30°时，则EF的长度为2．其中结论正确的有（ ）
如图，P为边长为2的正方形ABCD的对角线BD上任一点，过点P作PE⊥BC于点E，PF⊥CD于点F，连接EF．给出以下4个结论：①AP=EF；②AP⊥EF；③EF最短长度为$\sqrt{2}$；④若∠BAP=30°时，则EF的长度为2．其中结论正确的有（ ）| A． | ①②③ | B． | ①②④ | C． | ②③④ | D． | ①③④ |
19．
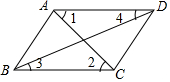如图，下列条件中，不能判定AD∥BC的是（ ）
如图，下列条件中，不能判定AD∥BC的是（ ）| A． | ∠1=∠2 | B． | ∠3=∠4 | C． | ∠ADC+∠DCB=180° | D． | ∠BAD+∠ADC=180° |