题目内容
18.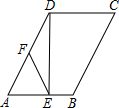 如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )
如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
分析 由直角三角形斜边上的中线性质得出EF=$\frac{1}{2}$AD=AF,由等腰三角形的性质得出∠FEA=∠A=65°,再由三角形内角和定理即可得出结果.
解答 解:∵DE⊥AB,
∴∠AED=90°,
∵点F为边AD上的中点,
∴EF=$\frac{1}{2}$AD=AF,
∴∠FEA=∠A=65°,
∴∠AFE=180°-∠A-∠FEA=50°.
故选:B.
点评 本题考查了直角三角形斜边上的中线性质、等腰三角形的性质、三角形内角和定理;由直角三角形斜边上的中线性质得出EF=AF是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.小明从一副扑克牌中取出3张红桃、2张黑桃共5张牌与弟弟做游戏,把这5张牌背面朝上洗匀后放在桌子上,小明与弟弟同时各抽一张,两人抽到花色相同的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
6.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为0.5?
7.不等式2x+4≤0的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
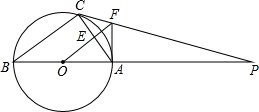 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.
如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF. 如图,排球在黑白两色的方砖上随机滚动,落在每块方砖上的可能性相同(若落在线上,则随机滚动一次).
如图,排球在黑白两色的方砖上随机滚动,落在每块方砖上的可能性相同(若落在线上,则随机滚动一次).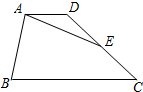 如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).
如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).