题目内容
7.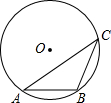 如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 作直径AD,连结BD,如图,根据圆周角定理得∠ABD=90°,则利用勾股定理可计算出BD=8,于是根据余弦定义得到cosD=$\frac{BD}{AD}$=$\frac{4}{5}$,然后利用圆周角定理易得cosC=$\frac{4}{5}$.
解答 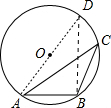 解:作直径AD,连结BD,如图,
解:作直径AD,连结BD,如图,
∵AD为直径,
∴∠ABD=90°,
在Rt△ABD中,∵AD=10,AB=6,
∴BD=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴cosD=$\frac{BD}{AD}$=$\frac{8}{10}$=$\frac{4}{5}$,
∵∠C=∠D,
∴cosC=$\frac{4}{5}$.
故选D.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了解直角三角形.

练习册系列答案
相关题目
17.下列因式分解正确的是( )
| A. | x3-x=x(x2-1) | B. | -a2+6a-9=-(a-3)2 | ||
| C. | x2+y2=(x+y)2 | D. | a3-2a2+a=a(a+1)(a-1) |
15.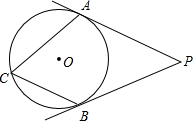 如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
 如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )| A. | 50° | B. | 65° | C. | 75° | D. | 130° |
2.四名运动员参加了射击预选赛,他们成绩的平均环数$\overline{x}$及其方差s2如下表所示,
如果选出一个成绩较好且状态稳定的人去参赛,那么应选( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 8.3 | 9.2 | 9.2 | 8.5 |
| s2 | 1 | 1 | 1.2 | 1.7 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
19.下列不等式变形正确的是( )
| A. | 由4x-1≥0得4x>1 | B. | 由5x>3 得 x>3 | C. | 由$\frac{y}{2}$>0得 y>0 | D. | 由-2x<4得x<-2 |
17.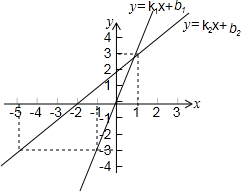 一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
 一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )| A. | x<-1 | B. | -5<x<1 | C. | -5<x<-1 | D. | -1<x<1 |