题目内容
15.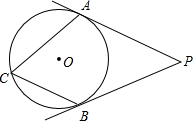 如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )
如图,P是⊙O外一点,PA、PB是⊙O的切线,∠APB=50°,点C在⊙O上,则∠ACB=( )| A. | 50° | B. | 65° | C. | 75° | D. | 130° |
分析 连结OA、OB,如图,先根据切线的性质得∠PAO=∠PBO=90°,再利用四边形的内角和得到可计算出∠AOB=180°-∠P=130°,然后根据圆周角定理即可得到∠ACB=$\frac{1}{2}$∠AOB=65°.
解答  解:连结OA、OB,如图,
解:连结OA、OB,如图,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∴∠AOB+∠P=180°,
∴∠AOB=180°-50°=130°,
∴∠ACB=$\frac{1}{2}$∠AOB=65°.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆周角定理.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
6.在-5,-$\frac{1}{10}$,-3.5,-0.01,-2,-212各数中,最大的数是( )
| A. | -212 | B. | -$\frac{1}{10}$ | C. | -0.01 | D. | -5 |
7.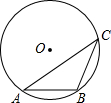 如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
 如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
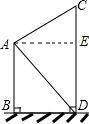 如图,甲楼的底端B处与乙楼的底端D处相距50m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为20°.从甲楼顶部A处看乙楼底部D处的俯角∠DAE的度数为35.分别求甲楼AB和乙楼CD的高为多少m(精确到1m).(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
如图,甲楼的底端B处与乙楼的底端D处相距50m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为20°.从甲楼顶部A处看乙楼底部D处的俯角∠DAE的度数为35.分别求甲楼AB和乙楼CD的高为多少m(精确到1m).(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70) 如图,小方格都是边长为1的正方形
如图,小方格都是边长为1的正方形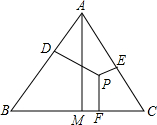 已知,如图所示:P为等边三角形ABC内的一点,它到三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高AM=h.则h与 h1、h2、h3有何数量关系?写出你的猜想并加以证明.
已知,如图所示:P为等边三角形ABC内的一点,它到三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高AM=h.则h与 h1、h2、h3有何数量关系?写出你的猜想并加以证明.