题目内容
12.先化简$\frac{{a}^{2}-6a+9}{4-2a}$÷($\frac{5}{a-2}$-a-2),再从±2、±3中选一个你认为合适的数代入求值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{(a-3)^{2}}{2(2-a)}$÷$\frac{-(a+3)(a-3)}{a-2}$=$\frac{(a-3)^{2}}{2(2-a)}$•$\frac{2-a}{(a+3)(a-3)}$=$\frac{a-3}{2(a+3)}$,
∵a-2≠0,a+3≠0,a-3≠0,
∴a≠2,a≠3,a≠-3,
则a=-2时,原式=-$\frac{5}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
7.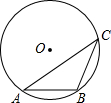 如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
 如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
17.估计$\sqrt{8}$在( )
| A. | 1~2之间 | B. | 2~3之间 | C. | 3~4之间 | D. | 4~5之间 |
1.如图,在4张背面完全相同的卡片上分别印有不同的图案.现将印有图案的一面朝下洗匀后,从中随机抽取一张,则抽出的卡片正面图案是中心对称图形的概率是( )

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 1 |
 如图,小方格都是边长为1的正方形
如图,小方格都是边长为1的正方形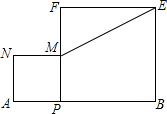 如图,线段AB=10,点P是AB的动点,分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF,连结ME,则ME的最小值是2$\sqrt{5}$.
如图,线段AB=10,点P是AB的动点,分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF,连结ME,则ME的最小值是2$\sqrt{5}$.