题目内容
18.若$\sqrt{m-3}+{(n+1)^2}$=0,则mn的值为$\frac{1}{3}$.分析 根据非负数的性质列式求出m、n的值,然后代入代数式进行计算即可得解.
解答 解:由题意得,m-3=0,n+1=0,
解得m=3,n=-1,
所以,mn=3-1=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
8.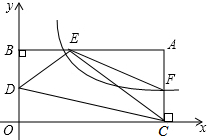 如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
 如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
6.在-5,-$\frac{1}{10}$,-3.5,-0.01,-2,-212各数中,最大的数是( )
| A. | -212 | B. | -$\frac{1}{10}$ | C. | -0.01 | D. | -5 |
7.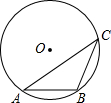 如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
 如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )
如图,在半径为5的⊙O中,弦AB=6,点C是优弧$\widehat{AB}$上一点(不与A,B重合),则cosC的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,小方格都是边长为1的正方形
如图,小方格都是边长为1的正方形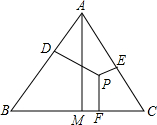 已知,如图所示:P为等边三角形ABC内的一点,它到三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高AM=h.则h与 h1、h2、h3有何数量关系?写出你的猜想并加以证明.
已知,如图所示:P为等边三角形ABC内的一点,它到三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高AM=h.则h与 h1、h2、h3有何数量关系?写出你的猜想并加以证明.