题目内容
4.将等腰三角形ABC折叠,使顶点B与底边AC的中点D重合,折线分别交AB,BC于点F,E,连接DF,DE.
(1)如图1,求证:四边形DFBE是菱形;
(2)如图2,延长FD至点G,使GD=DG,连接GC,并延长GC交FE的延长线于点H,在不添加任何辅助线的情况下,请直接写出图2中的所有平行四边形(不包括以BF为一边的平行四边形).
分析 (1)连接BD,交EF于点O,利用已知条件和折叠的性质证明BE=BF和EF与BD垂直平分,即可证明四边形DFBE是菱形;
(2)根据平行四边形的各种判定方法即可直接写出图2中的所有平行四边形.
解答 证明:(1)连接BD,交EF于点O,
∵AB=BC,点D是AC的中点,
∴BD⊥AC,∠ABD=∠DBC,
由折叠可知EF⊥BD,OB=OD,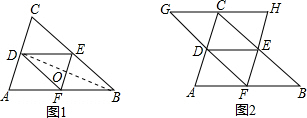
∴BE=BF,
∴OE=OF,
∴EF与BD垂直平分,
∴四边形DFBE是菱形;
(2)如图2中共有五个平行四边形(不包括以BF为一边的平行四边形).
分别是□ADEF;□ACHF;□DCHE;□DGCE;□DCEF.
点评 本题考查了菱形的判定和性质、平行四边形的判定和性质以及折叠的性质,题目的综合性较强,具有一定的开放性,解题的关键是熟记菱形、平行四边形的各种判定方法以及其各种性质.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
15.下列运算正确的是( )
| A. | 32•33=65 | B. | (2×102)(3×103)=6×106 | ||
| C. | (-xy)2•(xy)3=x5y5 | D. | (a4b)2=a4b2 |
12.若反比例函数y=-$\frac{4}{x}$的图象经过点(a,-a),则a的值为( )
| A. | ±2 | B. | -2 | C. | 2 | D. | 4 |
9.安徽省大力实施民生工程,自2007年到2015年资金投入达到3900亿元.3900亿元用科学记数法表示为( )
| A. | 3.9×103 | B. | 3.9×108 | C. | 39×108 | D. | 3.9×1011 |
14.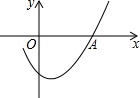 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )| A. | b2<4ac | B. | ac>0 | C. | 2a-b=0 | D. | a-b+c=0 |
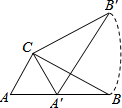 三角板∠ACB=90°,∠B=30°,BC=6,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边起始位置即停止转动,则B点转过的路径BB′的长为2π.
三角板∠ACB=90°,∠B=30°,BC=6,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边起始位置即停止转动,则B点转过的路径BB′的长为2π.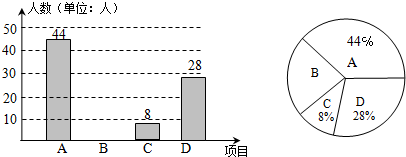
 如图,在?ABCD中,AB=4cm,BC=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=3cm.
如图,在?ABCD中,AB=4cm,BC=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=3cm.