题目内容
16.在我市初中开展的“阳光体育”活动中,某所中学七、八、九年级各有6个班级,每个班级人数为50左右,根据实际情况,决定开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种项目.为了解学生喜欢哪一种项目,该学校体育组随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请结合图中信息解答下列问题:(1)样本容量是100,请你为体育组提供一种较为合理的抽样方案;
(2)把条形统计图补充完整;
(3)该校贝贝、晶晶、洋洋和妮妮是学校的校园之星,现要从这四人的问卷中选出两人作为“阳光体育”运动形象代言人,问贝贝和晶晶同时被抽到的概率是多少?
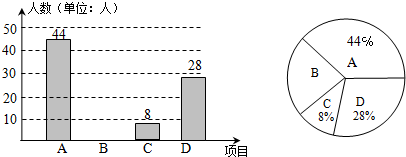
分析 (1)用D项目的人数除以该项目所占百分比即可得到样本容量;随机抽样即可;
(2)用样本容量分别减去A、C、D项目的人数得到B项目人数,然后补全条形统计图;
(3)先画出树状图展示所有12种等可能的结果数,再找出贝贝和晶晶同时被抽到的结果数,然后根据概率公式求解.
解答 解:(1)样本容量=28÷28%=100,
抽样方案可为:按照年级顺序依次抽取学号尾数为2或5的学生,抽取满100名为止;
故答案为100;
(2)B项目的人数=100-44-8-28=20(人),
如图,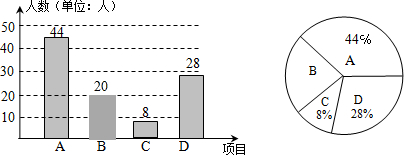
(3)画树状图为: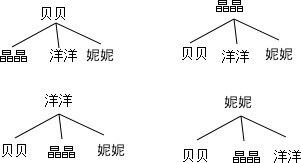
共有12种等可能的结果数,其中贝贝和晶晶同时被抽到的结果数为2,
所以贝贝和晶晶同时被抽到的概率=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了扇形统计图和条形统计图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.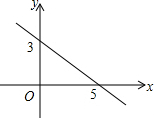 如图,一次函数y=kx+b的图象与两坐标轴交于两点,则不等式kx+b>0的解集是( )
如图,一次函数y=kx+b的图象与两坐标轴交于两点,则不等式kx+b>0的解集是( )
 如图,一次函数y=kx+b的图象与两坐标轴交于两点,则不等式kx+b>0的解集是( )
如图,一次函数y=kx+b的图象与两坐标轴交于两点,则不等式kx+b>0的解集是( )| A. | x<5 | B. | x>5 | C. | x<3 | D. | x>3 |
8.甲、乙两同学近期5次百米跑测试成绩的平均数相同,甲同学成绩的方差是5,乙同学成绩的方差是2.1,则对他们测试成绩的稳定性判断正确的是( )
| A. | 甲的成绩稳定 | B. | 乙的成绩较稳定 | ||
| C. | 甲、乙成绩的稳定性相同 | D. | 甲、乙成绩的稳定性无法比较 |
6. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )| A. | 60° | B. | 65° | C. | 55° | D. | 50° |
 如图,在菱形ABCD中,边长为10,∠A=60°,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是20;四边形A2015B2015C2015D2015的周长$\frac{5+5\sqrt{3}}{{2}^{1006}}$.
如图,在菱形ABCD中,边长为10,∠A=60°,顺次连接菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是20;四边形A2015B2015C2015D2015的周长$\frac{5+5\sqrt{3}}{{2}^{1006}}$.