题目内容
14.请两名工人制作广告牌,已知师傅单独做需4天完成,徒弟单独做需6天完成,现在徒弟先做1天,再两人合作,完成后共得到报酬450元.如果按各人完成工作量计算报酬,那么该如何分配?分析 设两人合作用了x天,根据题意列出方程,求出方程的解得到x的值,求出两人的工作量,即可做出判断.
解答 解:设两人合作用了x天,
根据题意得:$\frac{1}{6}$(x+1)+$\frac{1}{4}$x=1,
去分母得:2(x+1)+3x=12,
去括号得:2x+2+3x=12,
移项合并得:5x=10,
解得:x=2,
可得$\frac{1}{6}$×3=$\frac{1}{2}$,$\frac{1}{4}$×2=$\frac{1}{2}$,即两人的工作量相同,
则师傅与徒弟各分一半,即$\frac{1}{2}$×450=225元.
点评 此题考查了一元一次方程的应用,求出两人的工作量是解本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
2.已知关于x的一元二次方程x2+mx+n=0的两根为3和-4,则代数式x2-mx+n可分解为( )
| A. | (x-3)(x+4) | B. | (x+3)(x+4) | C. | (x+3)(x-4) | D. | (x-3)(x-4) |
4.绝对值大于6且小于9的所有整数有( )
| A. | 2 | B. | 3 | C. | 4 | D. | 无数个 |
9.下列对正方形的描述错误的是( )
| A. | 正方形的四个角都是直角 | B. | 正方形的对角线互相垂直 | ||
| C. | 邻边相等的矩形是正方形 | D. | 对角线相等的平行四边形是正方形 |
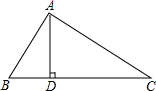 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠B=2∠C,若CD=8,求AB+BD的值.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠B=2∠C,若CD=8,求AB+BD的值.