题目内容
10.一个直角三角形的面积12S,两条直角边长的比为3:4,则这个直角三角形的两条直角边长分别为3$\sqrt{2S}$、4$\sqrt{2S}$(用含S的式子表示).分析 设两边长分别为3k、4k(k>0),然后利用三角形的面积公式可知:$\frac{1}{2}×3k×4k=12S$,从而可求得k,然后可求得两直角边长.
解答 解:设两边长分别为3k、4k(k>0).
根据题意得:$\frac{1}{2}×3k×4k=12S$,
解得:k=$\sqrt{2S}$.
所以3k=3$\sqrt{2S}$,4k=4$\sqrt{2S}$.
故答案为:3$\sqrt{2S}$,4$\sqrt{2S}$.
点评 本题主要考查的是算术平方根的应用,掌握算术平方根的定义是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
2.已知关于x的一元二次方程x2+mx+n=0的两根为3和-4,则代数式x2-mx+n可分解为( )
| A. | (x-3)(x+4) | B. | (x+3)(x+4) | C. | (x+3)(x-4) | D. | (x-3)(x-4) |
4.绝对值大于6且小于9的所有整数有( )
| A. | 2 | B. | 3 | C. | 4 | D. | 无数个 |
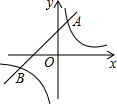 如图,函数y=$\frac{3}{x}$与函数y=x+2交于两点A(1,3),B(-3,-1),点P是y=$\frac{3}{x}$的图象上一点,当△AOP为等腰三角形时,求点P的坐标.
如图,函数y=$\frac{3}{x}$与函数y=x+2交于两点A(1,3),B(-3,-1),点P是y=$\frac{3}{x}$的图象上一点,当△AOP为等腰三角形时,求点P的坐标.