题目内容
5. 如图,点E在正方形ABCD的边CD上,若△ABE的面积为32,CE=6,则线段BE的长为10.
如图,点E在正方形ABCD的边CD上,若△ABE的面积为32,CE=6,则线段BE的长为10.
分析 根据正方形面积是△ABE面积的2倍,求出边长,再在RT△BCE中利用勾股定理求出BE的长即可.
解答 解:设正方形边长为a,
∵S△ABE=32,
∴S正方形ABCD=2S△ABE=64,
∴a2=64,
∵a>0,
∴a=8,
在RT△BCE中,∵BC=8,CE=6,∠C=90°,
∴BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=10.
故答案为10.
点评 本题考查正方形的性质、三角形的面积公式、勾股定理等知识,解题是关键是理解正方形面积是△ABE面积的2倍,属于中考常考题型.

练习册系列答案
相关题目
16. 如图,在正方形ABCD的外侧,作等边三角形AEB,则∠AED为( )
如图,在正方形ABCD的外侧,作等边三角形AEB,则∠AED为( )
 如图,在正方形ABCD的外侧,作等边三角形AEB,则∠AED为( )
如图,在正方形ABCD的外侧,作等边三角形AEB,则∠AED为( )| A. | 10° | B. | 15° | C. | 20° | D. | 125° |
20.“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )
| A. | 2.5×105 | B. | 2.5×10-5 | C. | 2.5×106 | D. | 2.5×10-6 |
10.三角形的两条边长分别为7和3,则第三边的长可以为( )
| A. | 3cm | B. | 10cm | C. | 4cm | D. | 7cm |
17. 如图,数轴上有四个点M,P,N,Q,若点M,N表示的数互为相反数,则图中表示绝对值最大的数对应的点是( )
如图,数轴上有四个点M,P,N,Q,若点M,N表示的数互为相反数,则图中表示绝对值最大的数对应的点是( )
 如图,数轴上有四个点M,P,N,Q,若点M,N表示的数互为相反数,则图中表示绝对值最大的数对应的点是( )
如图,数轴上有四个点M,P,N,Q,若点M,N表示的数互为相反数,则图中表示绝对值最大的数对应的点是( )| A. | 点M | B. | 点N | C. | 点P | D. | 点Q |
 如图所示,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,∠1=( )度.
如图所示,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,∠1=( )度.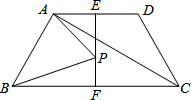 如图,在四边形ABCD中,AD∥BC,AB=CD且AB与CD不平行,AD=2,∠BCD=60°,对角线CA平分∠BCD,E,F分别是底边AD,BC的中点,连接EF,点P是EF上的任意一点,连接PA,PB,则PA+PB的最小值为2$\sqrt{3}$.
如图,在四边形ABCD中,AD∥BC,AB=CD且AB与CD不平行,AD=2,∠BCD=60°,对角线CA平分∠BCD,E,F分别是底边AD,BC的中点,连接EF,点P是EF上的任意一点,连接PA,PB,则PA+PB的最小值为2$\sqrt{3}$.