Question

15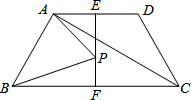．如图，在四边形ABCD中，AD∥BC，AB=CD且AB与CD不平行，AD=2，∠BCD=60°，对角线CA平分∠BCD，E，F分别是底边AD，BC的中点，连接EF，点P是EF上的任意一点，连接PA，PB，则PA+PB的最小值为2$\sqrt{3}$．

Answer 1

分析 要求PA+PB的最小值，PA、PB不能直接求，可考虑转化PA、PB的值，从而找出其最小值求解．

解答 解：∵E，F分别是底边AD，BC的中点，四边形ABCD是等腰梯形，
∴B点关于EF的对称点C点，
∴AC即为PA+PB的最小值，
∵∠BCD=60°，对角线AC平分∠BCD，
∴∠ABC=60°，∠BCA=30°，
∴∠BAC=90°，
∵AD=2，
∴PA+PB的最小值=AB•tan60°=2$\sqrt{3}$．
故答案为：2$\sqrt{3}$．

点评 本题考查了等腰梯形的性质和轴对称等知识的综合应用．综合运用这些知识是解决本题的关键．