题目内容
6.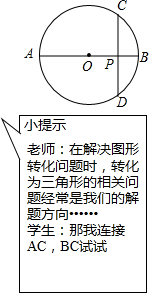 如图,CD是圆O的弦,AB是直径,且CD⊥AB,垂足为P.
如图,CD是圆O的弦,AB是直径,且CD⊥AB,垂足为P.(1)求证:PC2=PA•PB;
(2)PA=6,PC=3,求圆O的直径.
分析 (1)连接AC、BC,结合条件和垂径定理可证明△APC∽△CPB,利用相似三角形的性质可证得PC2=PA•PB;
(2)把PA、PC的长代入(1)中的结论,可求得PB,则可求得AB的长.
解答 (1)证明:
如图,连接AC、BC,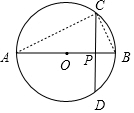
∵CD⊥AB,AB是直径,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠CAB=∠BCP,
∵∠CPA=∠CPB=90°,
∴△APC∽△CPB,
∴$\frac{PA}{PC}$=$\frac{PC}{PB}$,即PC2=PA•PB;
(2)解:
将PA=6,PC=3,代入PC2=PA•PB,可得32=6PB,
∴PB=1.5,
∴AB=PA+PB=6+1.5=7.5,
即圆的直径为7.5.
点评 本题主要考查相似三角形的判定和性质及垂径定理,利用条件构造三角形相似是解题的关键.

练习册系列答案
相关题目
16.光的速度约为3000 000千米/秒,用科学记数法表示为( )
| A. | 0.3×107 | B. | 3×106 | C. | 3×105 | D. | 30×104 |
14.把一个直径4毫米的手表零件,画在图纸上直径是8厘米,这幅图纸的比例尺是( )
| A. | 1:2 | B. | 2:1 | C. | 1:20 | D. | 20:1 |
11.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
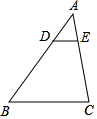 如图,DE∥BC,分别交△ABC的边AB、AC于点D、E,$\frac{AD}{AB}$=$\frac{1}{3}$,若AE=1,则EC=( )
如图,DE∥BC,分别交△ABC的边AB、AC于点D、E,$\frac{AD}{AB}$=$\frac{1}{3}$,若AE=1,则EC=( ) 如图,AB是⊙O的直径,点C在⊙O上,且点D在$\widehat{AC}$上.若∠AOC=134°,则∠BDC的大小为23度.
如图,AB是⊙O的直径,点C在⊙O上,且点D在$\widehat{AC}$上.若∠AOC=134°,则∠BDC的大小为23度.