题目内容
9．将一副直角三角板如图放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合，则α=75°．
分析 根据三角形的内角和求出∠2=45°，再根据对顶角相等求出∠3=∠2，然后根据三角形的一个外角等于与它不相邻的两个内角的和计算即可．
解答 解：
∵∠2=90°-45°=45°，
∴∠3=∠2=45°，
∴∠1=∠3+30°=45°+30°=75°．
故答案为：75°．
点评 本题考查的是三角形的内角和，三角形外角的性质，熟知三角形的一个外角等于与它不相邻的两个内角的和是解答此题的关键．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
11．在平面内，下列命题为真命题的是（ ）
| A． | 四条边相等的四边形是菱形 | B． | 对角线垂直的四边形是菱形 | ||
| C． | 对角线相等的四边形是矩形 | D． | 四个角相等的四边形是正方形 |
20．
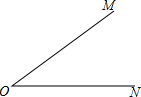已知∠MON=36°，先以O为圆心，任意长为半径画弧，分别交OM、ON于点A、B，再以A为圆心，AB长为半径画弧，交ON于点C，度量∠ACO的度数为（ ）
已知∠MON=36°，先以O为圆心，任意长为半径画弧，分别交OM、ON于点A、B，再以A为圆心，AB长为半径画弧，交ON于点C，度量∠ACO的度数为（ ）| A． | 36° | B． | 72° | C． | 108° | D． | 180° |
把下面的语句还原成图形：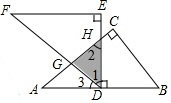
如图所示，将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，顶点D与边AB的中点重合，DE⊥AB交AC于点H，DF交AC于点G，则重叠部分（△DGH）的面积为$\frac{75}{16}$．
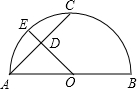如图，AB为半圆直径，O为圆心，C为半圆上一点，E是弧AC上的一点，且OE⊥AC交弦AC于点D．若AC=8cm，DE=2cm，求OD的长．
如图，已知⊙P的半径为1，圆心P在抛物线y=$\frac{1}{2}$x2-1上运动，当⊙P与x轴相切时，圆心P的坐标为（$\sqrt{2}$，1）或（-$\sqrt{2}$，1）或（0，-1）．