题目内容
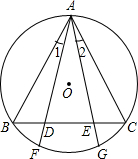△ABC内接于圆O，D、E在BC边上，且BD=CE，∠1=∠2．求证：AB=AC．考点：圆周角定理,全等三角形的判定与性质,圆心角、弧、弦的关系
专题：证明题
分析：连接BF，CG，根据∠1=∠2得出
=
，故
=
，BF=CG，所以∠DBF=∠ECG．根据SAS定理得出△BFD≌△CEG，由全等三角形的性质得出∠BFD=∠EGC，故
=
，由此可得出结论．
 |
| BF |
|
| CG |
|
| BG |
|
| CF |
|
| AB |
|
| AC |
解答：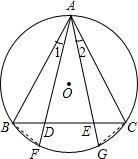
证明：连接BF，CG，
∵∠1=∠2，
∴
=
，
∴
=
∴BF=CG，
∴∠DBF=∠ECG．
在△BFD与△CEG中，
∵
∴△BFD≌△CEG
∴∠BFD=∠EGC，
∴
=
，
∴AB=AC．
证明：连接BF，CG，∵∠1=∠2，
∴
|
| BF |
|
| CG |
∴
|
| BG |
|
| CF |
∴BF=CG，
∴∠DBF=∠ECG．
在△BFD与△CEG中，
∵
|
∴△BFD≌△CEG
∴∠BFD=∠EGC，
∴
|
| AB |
|
| AC |
∴AB=AC．
点评：本题考查的是圆周角定理，熟知在同圆或等圆中同弧或等弧所对的圆周角相等是解答此题的关键．
练习册系列答案
走进文言文系列答案
相关题目
如图（1），已知AD是△ABC的中线，∠ADC=45°，把△ABC沿AD对折，点C落到点E的位置，连接BE，如图（2）
如图，E，F分别是正方形ABCD的边BC，CD边上的两点，∠1=∠2，求∠EAF的度数．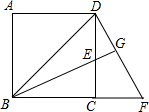
如图，已知正方形ABCD中，F为BC延长线上的一点，E为CD上的一点，CE=CF，BE的延长线交DF于点G．