题目内容
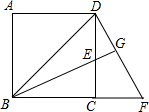 如图,已知正方形ABCD中,F为BC延长线上的一点,E为CD上的一点,CE=CF,BE的延长线交DF于点G.
如图,已知正方形ABCD中,F为BC延长线上的一点,E为CD上的一点,CE=CF,BE的延长线交DF于点G.(1)求证:BG⊥DF;
(2)若∠BEC=60°,求∠EFD的度数.
考点:全等三角形的判定与性质,正方形的性质
专题:
分析:(1)通过全等三角形△BCE≌△DCF的对应角∠EBC=∠FDC、对顶角∠BEC=∠DEG可以证得△BCE∽△DGE,然后由相似三角形的对应角相等推知∠BCE=∠DGE=90°,即BG⊥DF;
(2)首先根据全等三角形的性质可得∠CFD=∠BEC=60°,再计算出∠EFC的度数,根据角的和差关系可得答案.
(2)首先根据全等三角形的性质可得∠CFD=∠BEC=60°,再计算出∠EFC的度数,根据角的和差关系可得答案.
解答:(1)证明:∵四边形ABCD是正方形,
∴BC=CD,
在△BCE和△DCF中,
,
∴△BCE≌△DCF(SAS),
∴∠EBC=∠FDC(全等三角形的对应角相等),
即∠EBC=∠EDG,
又∵∠BEC=∠DEG,
∴△BCE∽△DGE,
∴∠BCE=∠DGE=90°(相似三角形的对应角相等),
即BG⊥DF;
(2)解:连接EF,
∵△BCE≌△DCF,
∴∠CFD=∠BEC=60°,
∵EC=CF,
∴∠EFC=∠CEF=(180°-90°)÷2=45°,
∴∠EFD=60°-45°=15°.
∴BC=CD,
在△BCE和△DCF中,
|

∴△BCE≌△DCF(SAS),
∴∠EBC=∠FDC(全等三角形的对应角相等),
即∠EBC=∠EDG,
又∵∠BEC=∠DEG,
∴△BCE∽△DGE,
∴∠BCE=∠DGE=90°(相似三角形的对应角相等),
即BG⊥DF;
(2)解:连接EF,
∵△BCE≌△DCF,
∴∠CFD=∠BEC=60°,
∵EC=CF,
∴∠EFC=∠CEF=(180°-90°)÷2=45°,
∴∠EFD=60°-45°=15°.
点评:此题主要考查了正方形的性质,全等三角形的判定和性质,关键是证明△BCE≌△DCF,掌握全等三角形对应角相等.

练习册系列答案
相关题目
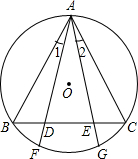 △ABC内接于圆O,D、E在BC边上,且BD=CE,∠1=∠2.求证:AB=AC.
△ABC内接于圆O,D、E在BC边上,且BD=CE,∠1=∠2.求证:AB=AC.