题目内容
已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(0,6),B(1,0),C(3,0).
(1)求出这个二次函数的表达式;
(2)写出它的顶点坐标和对称轴方程.
(1)求出这个二次函数的表达式;
(2)写出它的顶点坐标和对称轴方程.
考点:待定系数法求二次函数解析式,二次函数的性质
专题:计算题
分析:(1)将A,B,C三点坐标代入二次函数解析式求出a,b,c的值,即可确定出解析式;
(2)利用二次函数的性质求出顶点坐标与对称轴方程即可.
(2)利用二次函数的性质求出顶点坐标与对称轴方程即可.
解答:解:(1)根据题意设抛物线解析式为y=a(x-1)(x-3),
将A(0,6)代入得:6=3a,即a=2,
则二次函数解析式为y=2(x-1)(x-3)=2x2-8x+6;
(2)二次函数y=2x2-8x+6=2(x-2)2-2,
则顶点坐标为(2,-2),对称轴为直线x=2.
将A(0,6)代入得:6=3a,即a=2,
则二次函数解析式为y=2(x-1)(x-3)=2x2-8x+6;
(2)二次函数y=2x2-8x+6=2(x-2)2-2,
则顶点坐标为(2,-2),对称轴为直线x=2.
点评:此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
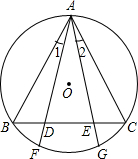 △ABC内接于圆O,D、E在BC边上,且BD=CE,∠1=∠2.求证:AB=AC.
△ABC内接于圆O,D、E在BC边上,且BD=CE,∠1=∠2.求证:AB=AC.