题目内容
 如图(1),已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落到点E的位置,连接BE,如图(2)
如图(1),已知AD是△ABC的中线,∠ADC=45°,把△ABC沿AD对折,点C落到点E的位置,连接BE,如图(2)(1)若线段BC=12cm,求线段BE的长度.
(2)在(1)的条件下,若线段AD=8cm,求四边形AEBD的面积.
考点:翻折变换(折叠问题)
专题:
分析:(1)根据三角形中线的定义得BD=CD=6,再根据折叠的性质得ED=CD=6,∠EDA=∠ADC=45°,则∠BDE=90°,于是可判断△BDE为等腰直角三角形,然后根据等腰直角三角形的性质计算BE的长;
(2)作AH⊥BC于H,如图(2),易得△ADH为等腰直角三角形,则AH=
AD=4
,于是可计算出S△ADC=12
,再根据折叠的性质得S△ADE=S△ADC=12
,然后利用四边形AEBD的面积=S△BDE+S△ADE=S△ADC进行计算.
(2)作AH⊥BC于H,如图(2),易得△ADH为等腰直角三角形,则AH=
| ||
| 2 |
| 2 |
| 2 |
| 2 |
解答: 解:(1)∵AD是△ABC的中线,BC=12,
解:(1)∵AD是△ABC的中线,BC=12,
∴BD=CD=6,
∵△ABC沿AD对折,点C落到点E的位置,
∴ED=CD=6,∠EDA=∠ADC=45°,
∴∠BDE=90°,
∴△BDE为等腰直角三角形,
∴BE=
BD=6
(cm);
(2)作AH⊥BC于H,如图(2),
∵∠ADC=45°,
∴△ADH为等腰直角三角形,
∴AH=
AD=
×8=4
,
∴S△ADC=
•AH•CD=
×4
×6=12
,
∵△ABC沿AD对折,点C落到点E的位置,
∴S△ADE=S△ADC=12
,
∴四边形AEBD的面积=S△BDE+S△ADE=S△ADC
=
×6×6+12
+12
=(18+24
)cm2.
 解:(1)∵AD是△ABC的中线,BC=12,
解:(1)∵AD是△ABC的中线,BC=12,∴BD=CD=6,
∵△ABC沿AD对折,点C落到点E的位置,
∴ED=CD=6,∠EDA=∠ADC=45°,
∴∠BDE=90°,
∴△BDE为等腰直角三角形,
∴BE=
| 2 |
| 2 |
(2)作AH⊥BC于H,如图(2),
∵∠ADC=45°,
∴△ADH为等腰直角三角形,
∴AH=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∵△ABC沿AD对折,点C落到点E的位置,
∴S△ADE=S△ADC=12
| 2 |
∴四边形AEBD的面积=S△BDE+S△ADE=S△ADC
=
| 1 |
| 2 |
| 2 |
| 2 |
=(18+24
| 2 |
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了等腰直角三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,长方形ABCD沿AE折叠,使点D落在BC边上的F点处,若BC=8cm,∠BAF=40°.求∠DAE的度数与AF的长度.
如图所示,长方形ABCD沿AE折叠,使点D落在BC边上的F点处,若BC=8cm,∠BAF=40°.求∠DAE的度数与AF的长度. 如图,在△ABC中,∠B=80°,∠C=40°,按要求完成下列各题:
如图,在△ABC中,∠B=80°,∠C=40°,按要求完成下列各题: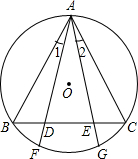 △ABC内接于圆O,D、E在BC边上,且BD=CE,∠1=∠2.求证:AB=AC.
△ABC内接于圆O,D、E在BC边上,且BD=CE,∠1=∠2.求证:AB=AC.