题目内容
 如图,AC是菱形ABCD的对角线,点M、N分别在边AD和BC上,BM、NM分别交AC于点E、F,AE=EF=FC,则△BMN与△ABC的面积比值是( )
如图,AC是菱形ABCD的对角线,点M、N分别在边AD和BC上,BM、NM分别交AC于点E、F,AE=EF=FC,则△BMN与△ABC的面积比值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:菱形的性质
专题:
分析:首先连接BD,由四边形ABCD是菱形,可得S△BCD=S△ABD=
S菱形ABCD,AD∥BC,则可证得△AEM∽△BEC,△AFM∽△CFN,然后由相似三角形的对应边成比例,易求得BN=
BC,然后由等高三角形的面积比等于对应底的比,求得答案.
| 1 |
| 2 |
| 3 |
| 4 |
解答: 解:连接BD,
解:连接BD,
∴四边形ABCD是菱形,
∴S△BCD=S△ABD=
S菱形ABCD,AD∥BC,
∴△AEM∽△BEC,△AFM∽△CFN,
∴
=
,
=
∵AE=EF=FC,
∴,
=
,
=2,
∴CN=
BC,
∴BN=
BC,
∴S△BMN=
S△BCD=
S△ABC.
∴S△BMN:S△ABC=
.
故选A.
 解:连接BD,
解:连接BD,∴四边形ABCD是菱形,
∴S△BCD=S△ABD=
| 1 |
| 2 |
∴△AEM∽△BEC,△AFM∽△CFN,
∴
| AM |
| BC |
| AE |
| CE |
| AM |
| CN |
| AF |
| CF |
∵AE=EF=FC,
∴,
| AM |
| BC |
| 1 |
| 2 |
| AM |
| CN |
∴CN=
| 1 |
| 4 |
∴BN=
| 3 |
| 4 |
∴S△BMN=
| 3 |
| 4 |
| 3 |
| 4 |
∴S△BMN:S△ABC=
| 3 |
| 4 |
故选A.
点评:此题考查了相似三角形的判定与性质以及菱形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
(-
×103)2×(1.5×104)2的计算结果是( )
| 2 |
| 3 |
| A、-1.5×1011 | ||
B、
| ||
| C、1014 | ||
| D、-1014 |
函数y=
变量x的取值范围是( )
| x | ||
|
| A、x>-3且x≠0 |
| B、x≠0 |
| C、x>3 |
| D、x≠-3或x≠0 |
已知样本:14、8、10、7、9、7、12、11、13、8、10、10、8、11、10、11、13、9、12、9,那么样本数据落在范围8.5~11.5内的频率( )
| A、0.52 | B、0.4 |
| C、0.25 | D、0.5 |
四边形ABCD为菱形,AC、BD为对角线,若AC=6,BD=8,则sin∠ABD的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,Rt△ABC中,∠ACB=90°,P为△ABC三条中线的交点,且∠BPC=90°,若AB=12,
如图,Rt△ABC中,∠ACB=90°,P为△ABC三条中线的交点,且∠BPC=90°,若AB=12, 如图,一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8 分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的关系如图所示.则下列说法正确的个数是( )
如图,一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8 分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的关系如图所示.则下列说法正确的个数是( )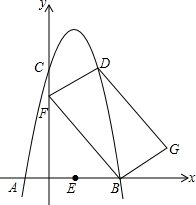 如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,
如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,