题目内容
四边形ABCD为菱形,AC、BD为对角线,若AC=6,BD=8,则sin∠ABD的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:菱形的性质,解直角三角形
专题:
分析:首先根据题意画出图形,由四边形ABCD为菱形,AC=6,BD=8,即可求得OA与OB的长,然后由勾股定理求得AB的长,继而求得答案.
解答: 解:四边形ABCD是菱形,
解:四边形ABCD是菱形,
∴AC⊥BD,OA=
AC=
×6=3,OB=
BD=
×8=4,
∴AB=
=5,
∴sin∠ABD=
=
.
故选B.
 解:四边形ABCD是菱形,
解:四边形ABCD是菱形,∴AC⊥BD,OA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=
| OA2+OB2 |
∴sin∠ABD=
| OA |
| AB |
| 3 |
| 5 |
故选B.
点评:此题考查了菱形的性质、三角函数的定义以及勾股定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
若两圆的半径分别为5cm和8cm,圆心距为3cm,则这两个圆的位置关系是( )
| A、内切 | B、相交 | C、外切 | D、外离 |
若反比例函数y=
的图象经过点(3,
),则k的值为( )
| k |
| x |
| 2 |
| 3 |
| A、6 | ||
B、
| ||
| C、2 | ||
| D、-2 |
下列运算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设a>0,b>0,c>0,且
+
+
=3,则以下说法正确的是( )
| b |
| a |
| c |
| b |
| a |
| c |
| A、a,b,c可能相等,也可能不等 |
| B、a,b,c相等 |
| C、a,b,c不相等 |
| D、以上说法都不对 |
 如图,∠AOB是直角,∠COD是直角,OE是∠BOC的平分线,∠EOD=15°则∠AOC=
如图,∠AOB是直角,∠COD是直角,OE是∠BOC的平分线,∠EOD=15°则∠AOC= 如图,AC是菱形ABCD的对角线,点M、N分别在边AD和BC上,BM、NM分别交AC于点E、F,AE=EF=FC,则△BMN与△ABC的面积比值是( )
如图,AC是菱形ABCD的对角线,点M、N分别在边AD和BC上,BM、NM分别交AC于点E、F,AE=EF=FC,则△BMN与△ABC的面积比值是( )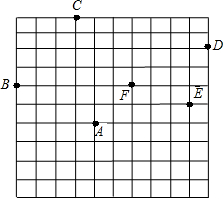 如图,小蚂蚁在10×10的方格上沿着网格线运动(每小格边长为1),一只小蚂蚁在A处找到食物后,要通知B,C,D,E处的其他小蚂蚁,规定其行动为:向上或向右走为正,向下或向左走为负.如果从A到B记为:A→B(-4,+2);从B到C记为:B→C(+3,+4)(第一个数表示左、右运动,第二个数表示上、下运动),那么:
如图,小蚂蚁在10×10的方格上沿着网格线运动(每小格边长为1),一只小蚂蚁在A处找到食物后,要通知B,C,D,E处的其他小蚂蚁,规定其行动为:向上或向右走为正,向下或向左走为负.如果从A到B记为:A→B(-4,+2);从B到C记为:B→C(+3,+4)(第一个数表示左、右运动,第二个数表示上、下运动),那么: