题目内容
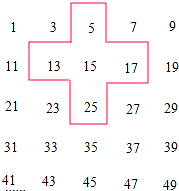 将连续奇数1,3,5,7,9,11,…,排成如下的数表,请回答下列问题:
将连续奇数1,3,5,7,9,11,…,排成如下的数表,请回答下列问题:(1)设设十字框中五个数的中间一个数为15,则十字框中的五个数之和为
(2)设十字框中五个数的中间一个数为x,若将十字框上下左右平移,可能住另外五个数,如果这五个数之和等于2015,则x=
考点:一元一次方程的应用
专题:
分析:(1)将十字框中的五个数相加即可;
(2)设十字框中五个数的中间一个数为x,根据这五个数之和等于2015列出方程,解方程即可.
(2)设十字框中五个数的中间一个数为x,根据这五个数之和等于2015列出方程,解方程即可.
解答:解:(1)5+13+15+17+25=75;
(2)设十字框中五个数的中间一个数为x,
依题意得:(x-10)+(x-2)+x+(x+2)+(x+10)=2015,
∴5x=2015,
∴x=403.
∵(403+1)÷2=202,
∴403是第202个数,
∵202÷5=40…2,
∴404在第41行,第2列.
因此这五个数分别是393,401,403,405,413.
故答案为75;403,41,2.
(2)设十字框中五个数的中间一个数为x,
依题意得:(x-10)+(x-2)+x+(x+2)+(x+10)=2015,
∴5x=2015,
∴x=403.
∵(403+1)÷2=202,
∴403是第202个数,
∵202÷5=40…2,
∴404在第41行,第2列.
因此这五个数分别是393,401,403,405,413.
故答案为75;403,41,2.
点评:此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
分式
与
的最简公分母是( )
| x |
| 3y |
| 3x |
| 2y2 |
| A、6y |
| B、3y2 |
| C、6y2 |
| D、6y3 |
2015的相反数是( )
A、-
| ||
| B、2015 | ||
C、
| ||
| D、-2015 |
 抛物线拱桥横截面如图所示,当水面宽4米时,拱顶离水面2米,若水面上升1米,则水面宽度将减少
抛物线拱桥横截面如图所示,当水面宽4米时,拱顶离水面2米,若水面上升1米,则水面宽度将减少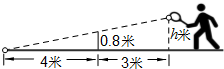 如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为
如图,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为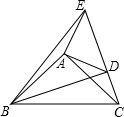 已知,如图在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE,以下四个结论:
已知,如图在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE,以下四个结论: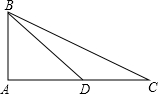 已知:如图,在△ABC中,∠A=90°,点D在边AC上,若∠ADB=45°,tan∠C=
已知:如图,在△ABC中,∠A=90°,点D在边AC上,若∠ADB=45°,tan∠C=