题目内容
 如图,已知梯形OABC的底边D在x轴上,CB∥OA,BA⊥OA,过点C的双曲线y=
如图,已知梯形OABC的底边D在x轴上,CB∥OA,BA⊥OA,过点C的双曲线y=| k |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:延长BA交y轴于E,过D作x轴的垂线,垂足为F,根据三角形的面积公式得出△OAB的面积=△OBE的面积,根据反比例函数系数k的几何意义得出△ODF的面积=△OCE的面积,则梯形DFAB的面积=△BOC的面积,再根据相似三角形的性质得出△OPF的面积=
梯形PFCB的面积,则
k=
,进而求出k的值.
| 1 |
| 8 |
| 1 |
| 2 |
| 3 |
| 8 |
解答: 解:延长BA交y轴于E,过D作x轴的垂线,垂足为F.
解:延长BA交y轴于E,过D作x轴的垂线,垂足为F.
由△OAB的面积=△OBE的面积,△ODF的面积=△OCE的面积,
∵OD:DB=1:2,
∴OD:OB=1:3,
∴△ODF的面积=
梯形DFAB的面积=
△BOC的面积=
×3=
,
即
k=
,
解得k=
.
故答案为
.
 解:延长BA交y轴于E,过D作x轴的垂线,垂足为F.
解:延长BA交y轴于E,过D作x轴的垂线,垂足为F.由△OAB的面积=△OBE的面积,△ODF的面积=△OCE的面积,
∵OD:DB=1:2,
∴OD:OB=1:3,
∴△ODF的面积=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 3 |
| 8 |
即
| 1 |
| 2 |
| 3 |
| 8 |
解得k=
| 3 |
| 4 |
故答案为
| 3 |
| 4 |
点评:本题考查了反比例系数k的几何意义.此题还可这样理解:当满足OD:DB=1:2时,点D在函数图象上运动,面积为定值.

练习册系列答案
相关题目
在平面直角坐标系中,点A和点B关于原点对称,已知点A的坐标为(2,3),那么点B的坐标为( )
| A、(3,-2) |
| B、(2,-3) |
| C、(-3,2) |
| D、(-2,-3) |
 如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是
如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是 把一块直尺与一块三角板如图放置,若∠1=30°,则∠2的度数为
把一块直尺与一块三角板如图放置,若∠1=30°,则∠2的度数为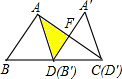 如图,在Rt△ABC中,AB=3,BC=5,∠BAC=90°,D是斜边BC的中点,将△ABD沿BC方向移动,使得点B与点D恰好重合,得到△A′B′D′,A′B′与AC相交于点F,则图中阴影部分(△ADF)的面积为
如图,在Rt△ABC中,AB=3,BC=5,∠BAC=90°,D是斜边BC的中点,将△ABD沿BC方向移动,使得点B与点D恰好重合,得到△A′B′D′,A′B′与AC相交于点F,则图中阴影部分(△ADF)的面积为 如图,O为矩形ABCD的中心(AB<BC),过O且互相垂直的两条直线被矩形四边所截,设截得的线段EF和GH长度分别为x,y,四边形EGFH的面积为S,当这两条直线保持垂直且围绕O点不停旋转时,下列说法正确的是( )
如图,O为矩形ABCD的中心(AB<BC),过O且互相垂直的两条直线被矩形四边所截,设截得的线段EF和GH长度分别为x,y,四边形EGFH的面积为S,当这两条直线保持垂直且围绕O点不停旋转时,下列说法正确的是( )