题目内容
15.甲、乙两名运动员在长50米的泳池里游泳.甲运动员的速度是1米/秒,乙运动员的速度是0.5米/秒.(1)他们同时分别在泳池的两端出发,进行50米短距离训练,几秒后他们相距20米?
(2)他们同时分别在泳池的两端出发,来回共游了5分钟,如果不计转向时间,那么这段时间里他们共相遇了多少次?
分析 (1)利用相遇前相距20m或相遇后相距20m,分别得出等式求出答案;
(2)利用两人行驶一个全程所用的时间结合总时间利用图形得出答案.
解答 解:(1)设x秒后他们相距20米.根据题意,得
(0.5+1)x=50-20或(0.5+1)x=50+20,
解得:x=20或$\frac{140}{3}$.
答:20秒或$\frac{140}{3}$秒后他们相距20米;
(2)甲游完一个全程用的时间:50÷1=50(秒),
乙游完一个全程要用的时间:50÷0.5=100(秒),
画出这两人的运行图:
图中实线段和虚线段的每个交点表示两运动员相遇了一次,从图上可以看出,甲、乙两运动员在5分钟内共相遇了5次,其中,有2次在游泳池的两端相遇.
答:在这段时间里共相遇了5次.
点评 此题主要考查了一元一次方程的应用,根据题意利用分类讨论得出是解题关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
6. 如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为( )
 如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为( )| A. | 2$\sqrt{3}$ | B. | 2 | C. | 4$\sqrt{3}$ | D. | $\sqrt{3}$ |
3.若|m|=3,n2=49,且m-n>0,则m+n的值是( )
| A. | 10 | B. | 4 | C. | -10或-4 | D. | 4或-4 |

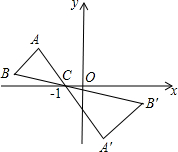 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,-1),则点B的坐标是(-3,$\frac{1}{2}$).
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,-1),则点B的坐标是(-3,$\frac{1}{2}$). 如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为135°.
如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为135°.