题目内容
10.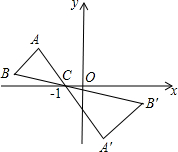 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,-1),则点B的坐标是(-3,$\frac{1}{2}$).
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,-1),则点B的坐标是(-3,$\frac{1}{2}$).
分析 作BD⊥x轴于D,B′D′⊥x轴于D′,根据相似三角形的性质求出CD,BD的长,得到点B的坐标.
解答 解: 作BD⊥x轴于D,B′D′⊥x轴于D′,
作BD⊥x轴于D,B′D′⊥x轴于D′,
∵点C的坐标是(-1,0),B′的坐标是(3,-1),
∴CD′=4,B′D′=1,
由题意得,△ABC∽A′B′C,相似比为1:2,
∴$\frac{BD}{B′D′}$=$\frac{CD}{CD′}$=$\frac{1}{2}$,
∴CD=2,BD=$\frac{1}{2}$,
∴点B的坐标是(-3,$\frac{1}{2}$).
故答案为:(-3,$\frac{1}{2}$).
点评 本题考查的是位似变换的性质和坐标与图形的性质,掌握位似的两个图形是相似形和相似三角形的性质是解题的关键.

练习册系列答案
相关题目
读句画图:如图,直线CD与直线AB相交于C,根据下列语句画图:
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.

5.若多项式x2+2ax+4能用完全平方公式进行因式分解,则a值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±4 |
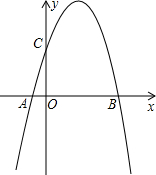 如图,在平面直角坐标系中,抛物线y=a2x+bx+4与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C.已知OA=1,OC=OB.
如图,在平面直角坐标系中,抛物线y=a2x+bx+4与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C.已知OA=1,OC=OB.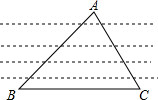 如图,为了测量河宽,在河的一边沿岸边选取B、C两点,在对岸岸边选择点A.测得∠B=45°,∠C=60°,BC=30米.求这条河的宽度(这里指点A到直线BC的距离).(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,为了测量河宽,在河的一边沿岸边选取B、C两点,在对岸岸边选择点A.测得∠B=45°,∠C=60°,BC=30米.求这条河的宽度(这里指点A到直线BC的距离).(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)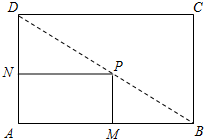 如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).
如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).