题目内容
4. 如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为135°.
如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为135°.
分析 连接DA、EA,根据线段垂直平分线的性质得到DA=DB,EA=EC,得到∠DAB=∠B,∠EAC=∠C,根据勾股定理的逆定理得到∠DAE=90°,根据三角形内角和定理计算即可.
解答 解: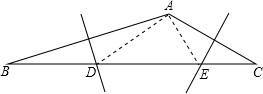 连接DA、EA,
连接DA、EA,
∵边AB、AC的垂直平分线分别交BC于点D、E,
∴DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∵BD2+CE2=DE2,
∴AD2+AE2=DE2,
∴∠DAE=90°,
∴2∠B+2∠C+90°=180°,
∴∠B+∠C=45°,
∴∠BAC=135°.
故答案为:135.
点评 本题考查的是线段垂直平分线的性质,掌握段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
9.双曲线$y=\frac{k}{x}$经过点(2,3),下列各点在该双曲线上的是( )
| A. | (6,-1) | B. | (-3,2) | C. | (3,-2) | D. | (-6,-1) |
16.下列说法不正确的是( )
| A. | 有一个角等于60°的两个等腰三角形相似 | |
| B. | 有一个底角等于30°的两个等腰三角形相似 | |
| C. | 有一个锐角相等的两个等腰三角形相似 | |
| D. | 有一个锐角相等的两个直角三角形相似 |
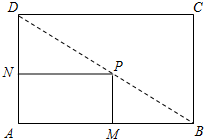 如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).
如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).