题目内容
6. 如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为( )
如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=30°,CD=6,则圆的半径长为( )| A. | 2$\sqrt{3}$ | B. | 2 | C. | 4$\sqrt{3}$ | D. | $\sqrt{3}$ |
分析 连接OC,由圆周角定理得出∠BOC=2∠A=60°,由垂径定理得出CE=DE=$\frac{1}{2}$CD=3,再由三角函数求出OC即可.
解答 解:连接OC,如图所示:
则∠BOC=2∠A=60°,
∵AB⊥CD,
∴CE=DE=$\frac{1}{2}$CD=3,
∵sin∠BOC=$\frac{CE}{OC}$,
∴OC=$\frac{CE}{sin60°}$=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$.
故选:A.
点评 本题考查了垂径定理、圆周角定理以及三角函数;熟练掌握圆周角定理,由垂径定理求出CE是解决问题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
16.下列说法不正确的是( )
| A. | 有一个角等于60°的两个等腰三角形相似 | |
| B. | 有一个底角等于30°的两个等腰三角形相似 | |
| C. | 有一个锐角相等的两个等腰三角形相似 | |
| D. | 有一个锐角相等的两个直角三角形相似 |

 B.
B.  C.
C.  D.
D. 
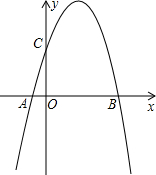 如图,在平面直角坐标系中,抛物线y=a2x+bx+4与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C.已知OA=1,OC=OB.
如图,在平面直角坐标系中,抛物线y=a2x+bx+4与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C.已知OA=1,OC=OB.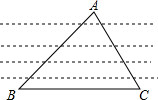 如图,为了测量河宽,在河的一边沿岸边选取B、C两点,在对岸岸边选择点A.测得∠B=45°,∠C=60°,BC=30米.求这条河的宽度(这里指点A到直线BC的距离).(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,为了测量河宽,在河的一边沿岸边选取B、C两点,在对岸岸边选择点A.测得∠B=45°,∠C=60°,BC=30米.求这条河的宽度(这里指点A到直线BC的距离).(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)