题目内容
 已知关于x的方程:x2-(m-1)x-m=0①和x2-(9-m)x+2(m+1)=3②,其中m>0.
已知关于x的方程:x2-(m-1)x-m=0①和x2-(9-m)x+2(m+1)=3②,其中m>0.(1)求证:方程①总有两个不相等的实数根;
(2)设二次函数y1=x2-(m-1)x-m的图象与x轴交于A、B两点(点A在点B的左侧),将A、B两点按照相同的方式平移后,点A落在点A′(1,3)处,点B落在点B′处,若点B′的横坐标恰好是方程②的一个根,求m的值;
(3)设二次函数y2=x2-(9-m)x+2(m+1),在(2)的条件下,函数y1,y2的图象位于直线x=3左侧的部分与直线y=kx(k>0)交于两点,当向上平移直线y=kx时,交点位置随之变化,若交点间的距离始终不变,则k的值是
考点:抛物线与x轴的交点,根的判别式,一次函数图象与几何变换,坐标与图形变化-平移
专题:
分析:(1)依据根的判别式△>0即可判定.
(2)根据解析式求得与x轴的交点A(-1,0),B(m,0),平移后,点A落在点A'(1,3)处,则平移方式是将点A向右平移2个单位,再向上平移3个单位得到,所以点B平移后的点B为(m+2,3),代入x2-(9-m)x+2(m+1)②,即可求得m的值.
(3)由(2)可知m=3,所以抛物线的解析式可求出,进而可求出两个抛物线的交点坐标,再由条件向上平移直线y=kx时,交点位置随之变化,若交点间的距离始终不变,即可求出k的值.
(2)根据解析式求得与x轴的交点A(-1,0),B(m,0),平移后,点A落在点A'(1,3)处,则平移方式是将点A向右平移2个单位,再向上平移3个单位得到,所以点B平移后的点B为(m+2,3),代入x2-(9-m)x+2(m+1)②,即可求得m的值.
(3)由(2)可知m=3,所以抛物线的解析式可求出,进而可求出两个抛物线的交点坐标,再由条件向上平移直线y=kx时,交点位置随之变化,若交点间的距离始终不变,即可求出k的值.
解答:解:(1)方程x2-(m-1)x-m=0中,
△=(m-1)2+4m=m2+2m+1=(m+1)2,
由m>0知必有m+1>0,故△>0.∴方程①总有两个不相等的实数根;
(2)令y1=0,依题意可解得A(-1,0),B(m,0).
∵平移后,点A落在点A'(1,3)处,
∴平移方式是将点A向右平移2个单位,再向上平移3个单位得到.
∴点B(m,0)按相同的方式平移后,点B'为(m+2,3).
则依题意有(m+2)2-(9-m)(m+2)+2(m+1)=3.
解得m1=3,m2=-
(负数舍去).
∴m的值为3.
(3)∵m=3,
∴y1=x2-2x-3,y2=x2-6x+8,
∴y1与y=kx的交点坐标为:
,y2与y=kx的交点坐标为
,
又∵向上平移直线y=kx时,交点位置随之变化,若交点间的距离始终不变,
∴k=
.
故答案为:
.
△=(m-1)2+4m=m2+2m+1=(m+1)2,
由m>0知必有m+1>0,故△>0.∴方程①总有两个不相等的实数根;
(2)令y1=0,依题意可解得A(-1,0),B(m,0).
∵平移后,点A落在点A'(1,3)处,
∴平移方式是将点A向右平移2个单位,再向上平移3个单位得到.
∴点B(m,0)按相同的方式平移后,点B'为(m+2,3).
则依题意有(m+2)2-(9-m)(m+2)+2(m+1)=3.
解得m1=3,m2=-
| 5 |
| 2 |
∴m的值为3.
(3)∵m=3,
∴y1=x2-2x-3,y2=x2-6x+8,
∴y1与y=kx的交点坐标为:
|
|
又∵向上平移直线y=kx时,交点位置随之变化,若交点间的距离始终不变,
∴k=
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查了二次函数的综合运用,用到的知识点有根的判别式的运用、平移的性质以及函数图象交点的问题,题目的综合性较强,对学生的综合解题能力要求很高,是一道不错的中考题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
下面计算(-7+a+b)(-7-a-b)正确的是( )
| A、原式=[-(-7-a-b)][-(7+a+b)]=72-(a+b)2 |
| B、原式=[-(-7+a)+b][-(7+a)-b]=(7+a)2-b2 |
| C、原式=(-7+a+b)[-7-(a+b)]=-72-(a+b)2 |
| D、原式=(-7+a+b)[-7-(a+b)]=72+(a+b)2 |
 如图,在Rt△ABC中,∠ABC=90°,AC=10cm,点D为AC的中点,则BD=
如图,在Rt△ABC中,∠ABC=90°,AC=10cm,点D为AC的中点,则BD=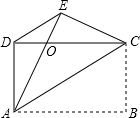 如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.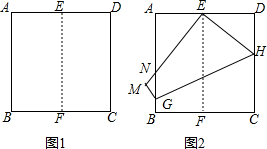 如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE=
如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE=