题目内容

如图所示，AB∥CD，∠D=27°，∠E=36°，则∠ABE的度数是
 
．
考点：平行线的性质
专题：
分析：先根据三角形外角性质得∠BFD=∠E+∠D=63°，然后根据平行线的性质得到∠ABE=∠BFD=63°．
解答：解：如图，
∵∠BFD=∠E+∠D，
而∠D=27°，∠E=36°，
∴∠BFD=36°+27°=63°，
∵AB∥CD，
∴∠ABE=∠BFD=63°．
故答案为：63°．
点评：本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
相关题目
若点（m，n）在一次函数y=2x-3的图象上．
（1）求代数式3n-6m+2023的值；
（2）点A（5m-6，5n）在直线y=2x-3上吗？为什么？
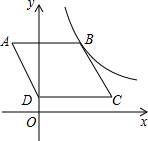 如图，已知?ABCD水平放置在平面直角坐标系xOy中，若点A，D的坐标分别为（-2，5），（0，1），点B（3，5）在反比例函数y=
k
x
（x＞0）图象上．
（1）求反比例函数y=
k
x
的解析式；
（2）将?ABCD沿x轴正方向平移10个单位后，能否使点C落在反比例函数y=
k
x
的图象上？并说明理由．
已知a2-b2=-
1
6
，a-b=
1
2
，则
a+b
a-b
=
 
．
已知一次函数y=ax+b中，x和y的部分对应值如表：
x -2 -1 0 1.5 2 3
y 6 4 2 -1 -2 -4
那么方程ax+b=0的解是
 
．
如图，直线AB∥CD，∠EFA=30°，∠FGH=90°，∠HMN=30°，∠CNP=50°，则∠GHM的度数为
 
．
已知平面上四点A（0，0），B（10，0），C（10，6），D（0，6），直线y=mx-3m将四边形ABCD分成面积相等的两部分，则m的值为
 
．
△ABC中，∠C=90°，AB=c，BC=a，AC=b，若a：c=
2
：
3
，c=6
3
，则b=
 
．
若a＜b，则下列各式中一定正确的是（　　）
A、ab＜0B、ab＞0
C、a-b＞0D、-a＞-b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网