题目内容
若关于x的多项式(x2＋x－n)(mx－3)的展开式中不含x2和常数项，求m，n的值．
m＝3，n＝0. 【解析】试题分析：本题考查了利用多项式的不含问题求字母的值，先按照多项式与多项式的乘法法则乘开，再合并关于x的同类项，然后令不含项的系数等于零，列方程求解即可. 【解析】 原式＝mx3＋(m－3)x2－(3＋mn)x＋3n， 由展开式中不含x2和常数项，得到m－3＝0，3n＝0， 解得m＝3，n＝0.
练习册系列答案
相关题目
元旦期间，为了满足颍上县百姓的消费需要，某大型商场计划用170000元购进一批家电，这批家里的进价和售价如表：
类别 | 彩电 | 冰箱 | 洗衣机 |
进价（元/台） | 2000 | 1600 | 1000 |
售价（元/台） | 2300 | 1800 | 1100 |
若在现有资金允许的范围内，购买表中三类家电共100台，其中彩电台数是冰箱台数的2倍，设该商场购买冰箱x台．
（1）用含x的代数式表示洗衣机的台数．
（2）商场至多可以购买冰箱多少台？
（3）购买冰箱多少台时，能使商场销售完这批家电后获得的利润最大？最大利润为多少元？
（1）﹣3x+100台；（2）26台；（3）23000元 【解析】试题分析：（1）根据彩电台数+冰箱台数+洗衣机台数=100，即可用含x的代数式表示洗衣机的台数； （2）根据总价=单价×数量，可列出关于x的一元一次不等式，解不等式即可得出x的取值范围，根据x为正整数即可得出结论； （3）设该商场的利润为W，根据利润=单台利润×数量可列出W关于x的函数关系式，根据一次函数的性质结合（2）的...
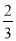]＝0，[3.14]＝3.按此规定[
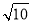＋1]的值为（ ）