题目内容
18.在平面直角坐标系中有两条直线l1、l2,直线l1相应的函数表达式为y=x-2.如果将图形翻折,使直线l1与l2重合,此时点(-1,0)与点(0,-1)也重合,求直线l2相应的函数表达式.分析 分别令x=0、y=0得出直线l1与坐标轴的两交点,再根据翻折时点(-1,0)与点(0,-1)重合,可得出两交点翻折后重合点的坐标,由点的坐标结合待定系数法即可求出直线l2相应的函数表达式.
解答 解:依照题意画出图形,如图所示.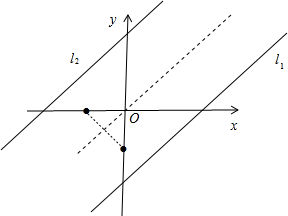
令x=0,则y=-2,
即直线l1与y轴的交点为(0,-2).
∵将图形翻折后点(-1,0)与点(0,-1)重合,
∴点(0,-2)经翻折后与点(-2,0)重合.
令y=0,则有x-2=0,解得:x=2,
即直线l1与x轴的交点为(2,0).
点(2,0)经翻折后与点(0,2)重合.
设直线l2相应的函数表达式为y=kx+b,
则有$\left\{\begin{array}{l}{0=-2k+b}\\{2=b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$.
故直线l2相应的函数表达式为y=x+2.
点评 本题考查了一次函数图象与几何变换以及待定系数法求函数解析式,解题的关键是根据翻折的规则找出直线l2上的两点坐标.本题属于基础题,难度不大,解决该题型题目时,找出翻折前图象与坐标轴的交点坐标,依照翻折点的变化规律找出翻折后该两点对应的坐标,再由待定系数法即可解决问题.若本题为填空或者选择,直角画出函数图象可直接根据平移直线得出直线l2相应的函数表达式.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
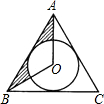 如图,已知等边三角形ABC的边长是6,⊙O是它的内切圆,则图中阴影部分的面积是3$\sqrt{3}$-π.
如图,已知等边三角形ABC的边长是6,⊙O是它的内切圆,则图中阴影部分的面积是3$\sqrt{3}$-π.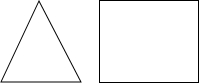 一个几何体的主视图和左视图如图所示,它是什么几何体?请补画这个几何体的俯视图.
一个几何体的主视图和左视图如图所示,它是什么几何体?请补画这个几何体的俯视图.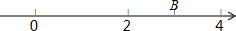 实数a在数轴上的位置点B如图所示,化简|a-2|+$\sqrt{(a-4)^{2}}$.
实数a在数轴上的位置点B如图所示,化简|a-2|+$\sqrt{(a-4)^{2}}$.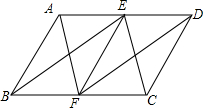 如图,在?ABCD中,E,F分别为AD,BC的中点,连接EF,AF,BE,CE,DF,则图中和四边形ABFE面积相等的四边形有( )个.
如图,在?ABCD中,E,F分别为AD,BC的中点,连接EF,AF,BE,CE,DF,则图中和四边形ABFE面积相等的四边形有( )个. 如图,已知四边形ABCD是平行四边形,AB<AD.
如图,已知四边形ABCD是平行四边形,AB<AD.