题目内容
5．
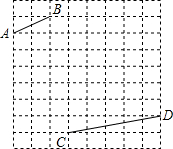如图的方格纸中，每个小正方形的边长均为1，有线段AB和线段CD，线段的端点均在小正方形的顶点上．（1）在方格纸中画出分别以线段AB，CD为一边的两个三角形，使这两个三角形关于某条直线成轴对称，且两个三角形的顶点均在小正方形的顶点上．
（2）请直接写出一个三角形的面积．
分析 （1）利用轴对称图形的性质结合网格，以正方形对角线为对称轴，得出对应点位置进而得出答案；
（2）利用三角形所在矩形减去周围三角形面积进而求出即可．
解答 解：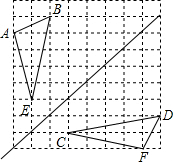
（1）如图所示：△ABE和△EDC即为所求；
（2）S△AEB=2×5-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×5-$\frac{1}{2}$×1×4=$\frac{9}{2}$．
点评 此题主要考查了轴对称变换和三角形面积求法，根据题意得出对应点位置是解题关键．
练习册系列答案
相关题目
16．若$\sqrt{b}$=2，$\root{3}{a}$=-3，则b-a的值是（ ）
| A． | 31 | B． | -31 | C． | 29 | D． | -30 |
13．已知A（1，y1）、B（2，y2）、C（-3，y3）都在反比例函数y=$\frac{2}{x}$的图象上，则y1、y2、y3的大小关系的是（ ）
| A． | y2＞y1＞y3 | B． | y1＞y2＞y3 | C． | y3＞y2＞y1 | D． | y1＞y3＞y2 |
10．$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$和$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$都是方程y=kx+b的解，则k，b的值分别为（ ）
| A． | 6，3 | B． | 1，4 | C． | 3，2 | D． | -1，3 |
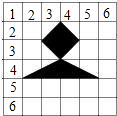小明在玩一种叫“掷飞镖”的游戏，如果小明将镖随意投中如图所示的正方形木板，那么镖落在阴影部分的概率是$\frac{1}{9}$．
15．
如图，将Rt△ABC绕直角顶点顺时针旋转90°，得到△A′B′C，连接AA′，若∠1=22°，则∠B的度数是（ ）
如图，将Rt△ABC绕直角顶点顺时针旋转90°，得到△A′B′C，连接AA′，若∠1=22°，则∠B的度数是（ ）| A． | 67° | B． | 62° | C． | 82° | D． | 72° |