题目内容
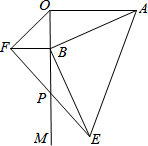 如图,AO⊥OM,OA=8
如图,AO⊥OM,OA=8| 2 |
| A、4 | ||
B、4
| ||
C、6
| ||
| D、BP的长度随B点的运动而变化 |
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:如图,作辅助线,首先证明△ABO≌△BEN,得到BO=ME;进而证明△BPF≌△MPE,即可解决问题.
解答: 解:如图,过点E作EN⊥BM,垂足为点N;
解:如图,过点E作EN⊥BM,垂足为点N;
∵∠AOB=∠ABE=∠BME=90°,
∴∠ABO+∠BAO=∠ABO+∠MBE,
∴∠BAO=∠MBE;
∵△ABE、△BFO均为等腰直角三角形,
∴AB=BE,BF=BO;
在△ABO与△BEN中,
,
∴△ABO≌△BEN(AAS),
∴BO=ME,BM=AO;而BO=BF,
∴BF=ME;
在△BPF与△MPE中,
,
∴△BPF≌△MPE(AAS),
∴BP=MP=
BM;而BM=AO,
∴BP=
AO=
×8
=4
,为定值;
故选:B.
 解:如图,过点E作EN⊥BM,垂足为点N;
解:如图,过点E作EN⊥BM,垂足为点N;∵∠AOB=∠ABE=∠BME=90°,
∴∠ABO+∠BAO=∠ABO+∠MBE,
∴∠BAO=∠MBE;
∵△ABE、△BFO均为等腰直角三角形,
∴AB=BE,BF=BO;
在△ABO与△BEN中,
|
∴△ABO≌△BEN(AAS),
∴BO=ME,BM=AO;而BO=BF,
∴BF=ME;
在△BPF与△MPE中,
|
∴△BPF≌△MPE(AAS),
∴BP=MP=
| 1 |
| 2 |
∴BP=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故选:B.
点评:该命题以三角形为载体,以全等三角形的判定及其性质的应用为考查的核心构造而成;解题的关键是作辅助线,构造全等三角形,灵活运用有关定理来分析、判断或解答.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,CD是切线,AC⊥CD,DE⊥AB,求证:DE2=AC•FC.
如图,AB是⊙O的直径,CD是切线,AC⊥CD,DE⊥AB,求证:DE2=AC•FC. 已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD.
已知:如图,CB=DE,∠B=∠E,∠BAE=∠CAD.