题目内容
6.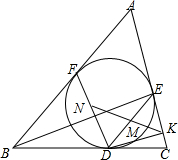 设△ABC的内切圆与BC、CA、AB分别切于D、E、F,M、N分别为DE、DF的中点,直线MN与CA交于K.求证:DK∥BE.
设△ABC的内切圆与BC、CA、AB分别切于D、E、F,M、N分别为DE、DF的中点,直线MN与CA交于K.求证:DK∥BE.
分析 连接OB、OC、OD,由切线的性质得出OD⊥BC,由切线长定理和等腰三角形的性质得出得出DF⊥OB,DE⊥OC,由射影定理得出ON•OB=OD2=OM•OC,得出B、C、M、N四点共圆,由圆周角定理得出∠KMC=∠OBC,证明△KMC∽△OCB,得出比例式$\frac{CK}{OC}=\frac{CM}{BC}$,得出$\frac{CK}{CE}=\frac{CK}{OC}•\frac{OC}{CE}=\frac{CM}{BC}•\frac{OC}{CD}$,由射影定理得出CD2=CM•OC,得出比例式,即可得出结论.
解答 证明:连接OB、OC、OD,如图所示: 则OD⊥BC,
则OD⊥BC,
由切线长定理得:BD=BF,∠OBD=∠OBF,CD=CE,∠OCD=∠OCE,
∴DF⊥OB,DE⊥OC,
由射影定理得:ON•OB=OD2=OM•OC,
∴B、C、M、N四点共圆,
∴∠KMC=∠OBC,
∵∠KCM=∠OCB,
∴△KMC∽△OCB,
∴$\frac{CK}{OC}=\frac{CM}{BC}$,
∴$\frac{CK}{CE}=\frac{CK}{OC}•\frac{OC}{CE}=\frac{CM}{BC}•\frac{OC}{CD}$,
∵∠ODC=90°,DM⊥OC,
∴CD2=CM•OC,
∴$\frac{CK}{CE}=\frac{CM•OC}{BC•CD}=\frac{CD}{BC}$,
∴DK∥BE.
点评 本题考查了三角形的内切圆、切线的性质、切线长定理、射影定理、平行线的判定、相似三角形的判定与性质、圆周角定理等知识;本题综合性强,难度较大,需要通过作辅助线运用射影定理和三角形相似才能得出结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列命题正确的是( )
| A. | 相等的圆周角对的弧相等 | B. | 等弧所对的弦相等 | ||
| C. | 三点确定一个圆 | D. | 平分弦的直径垂直于弦 |
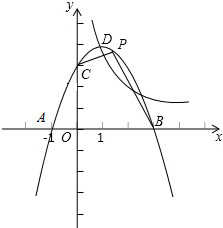 如图,抛物线y=ax2+bx+3与x轴交于A、B两点(A在B的左边),与y轴交于C,tan∠CAB=3;双曲线$y=\frac{k}{x}$(k≠0)经过抛物线y=ax2+bx+3的顶点,点D的横坐标为1.
如图,抛物线y=ax2+bx+3与x轴交于A、B两点(A在B的左边),与y轴交于C,tan∠CAB=3;双曲线$y=\frac{k}{x}$(k≠0)经过抛物线y=ax2+bx+3的顶点,点D的横坐标为1.
 如图,在△ABC中,∠C=90°,AB=12,AD是△ABC的一条角平分线.若CD=4,则△ABD的面积为24.
如图,在△ABC中,∠C=90°,AB=12,AD是△ABC的一条角平分线.若CD=4,则△ABD的面积为24.
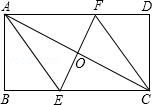 将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,